Radiografía de datos con dlookr: más allá del summary().

Limpia, fija y da esplendor

Introducción al paquete dlookr aplicado a un dataset de un estudio descriptivo

Autor/a

Antonio Matas-Terrón

Fecha de publicación

8 abril 2025

1 Programador y mantenimiento

Nombre: Choonghyun Ryu
Contacto: choonghyun.ryu@gmail.com
GitHub: choonghyunryu/dlookr
Origen: El término dlookr sintetiza “looking at the data”.
Versión 0.6.3 publicada en CRAN
Fecha: 7 de febrero de 2024

2 Introducción a la librería dlookr de R

dlookr es una colección de herramientas que trata de facilitar el diagnóstico, exploración y transformación de datos.
Ofrece información y visualizaciones de valores faltantes, valores atípicos, valores únicos y negativos, etc., ayudando a entender la distribución y calidad de los datos.
Más información sobre la librería en: https://cran.r-project.org/web/packages/dlookr/index.html

2.1 Diagnostica, explora…

Diagnóstico:
- Datos categóricos.
- Numéricos.
- Outliers.
- Valores perdidos.

Explora:
- Estadísticos descriptivos.
- Comprobación de la normalidad.
- Comprobación de la asimetría (skewness).
- Correlación.

2.2 Diagnostica, explora y repara

Imputación en datos perdidos numéricos:
- Media.
- Mediana.
- Moda.
- knn.

Imputación en datos perdidos categóricos:
- Moda.
- rpart (recursive partitioning and regression trees).
- mice (multivariate imputation by chained equations).

2.3 Diagnostica, explora y repara

Imputación en outliers:
- Media.
- Mediana.
- Moda.
- Capado.
Agrupamiento (binning).

2.4 Instalación

# Instalación desde R.

install.packages("dlookr", dependencies = T)

# Versión de desarollo

# devtools::install_github("choonghyunryu/dlookr")

# Si no puede usar R o Rstudio, puede recurrirse al servicio de Posit en la nube:

# https://posit.cloud/

2.5 Cargando paquetes

library(tidyverse)
library(dlookr)
library(readr) # Para leer los datos
library(flextable) # No necesario
library(gridExtra) # No necesario

2.6 Dataset de ejemplo

Una historia de nuestros datos:

El cuestionario CUDAD trata de recoger datos sobre la actitud del alumnado de Educación a la formación de datos y a las asignaturas de metodología de investigación en Educación.
Como es típico (en CCSS) está lleno de variables ordinales y casi ninguna variable escalar.

El dataset está disponible en: Repositorio Gitlab

dfm <- read_delim("https://gitlab.com/amataste/dlookr_sesion_grupormalaga/-/raw/main/dataset_ejercicios.csv",
  delim = "\t"
)
# View(dfm)

3 Diagnóstico

3.1 Sintaxis para el diagnóstico

Diagnóstico de los datos:

diagnose(dataset)
diagnose(dataset, variable1, variable2,…) o alternativamente -variable
Las variables se pueden indicar por el nombre o por la posición en el dataset

3.2 Sintaxis para el diagnóstico: general

diagnose(dfm)

# A tibble: 39 × 6
   variables   types     missing_count missing_percent unique_count unique_rate
   <chr>       <chr>             <int>           <dbl>        <int>       <dbl>
 1 N           numeric               0           0              243      1     
 2 Universidad character             0           0                3      0.0123
 3 Sexo        character             2           0.823            3      0.0123
 4 Edad        numeric               5           2.06            14      0.0576
 5 Estudios    character             2           0.823            6      0.0247
 6 Curso       numeric               0           0                5      0.0206
 7 V1          numeric               6           2.47             7      0.0288
 8 V2          numeric              57          23.5              7      0.0288
 9 V3          numeric              34          14.0              7      0.0288
10 V4          numeric               0           0                6      0.0247
# ℹ 29 more rows

3.3 Sintaxis para el diagnóstico: algunas variables

diagnose(dfm, 2, 3, 7:10)

# A tibble: 6 × 6
  variables   types     missing_count missing_percent unique_count unique_rate
  <chr>       <chr>             <int>           <dbl>        <int>       <dbl>
1 Universidad character             0           0                3      0.0123
2 Sexo        character             2           0.823            3      0.0123
3 V1          numeric               6           2.47             7      0.0288
4 V2          numeric              57          23.5              7      0.0288
5 V3          numeric              34          14.0              7      0.0288
6 V4          numeric               0           0                6      0.0247

3.4 Sintaxis para el diagnóstico: por grupos

Por grupos, complementándose con dplyr

dfm %>%
  group_by(Sexo) %>%
  diagnose(2, 7:10)

# A tibble: 15 × 8
   variables   types Sexo  data_count missing_count missing_percent unique_count
   <chr>       <chr> <chr>      <int>         <dbl>           <dbl>        <int>
 1 Universidad char… F            213             0            0               3
 2 Universidad char… M             28             0            0               3
 3 Universidad char… <NA>           2             0            0               1
 4 V1          nume… F            213             5            2.35            7
 5 V1          nume… M             28             1            3.57            6
 6 V1          nume… <NA>           2             0            0               1
 7 V2          nume… F            213            49           23.0             7
 8 V2          nume… M             28             8           28.6             6
 9 V2          nume… <NA>           2             0            0               1
10 V3          nume… F            213            31           14.6             7
11 V3          nume… M             28             3           10.7             7
12 V3          nume… <NA>           2             0            0               2
13 V4          nume… F            213             0            0               6
14 V4          nume… M             28             0            0               5
15 V4          nume… <NA>           2             0            0               1
# ℹ 1 more variable: unique_rate <dbl>

3.5 Sintaxis para el diagnóstico: variables numéricas

Sólo analizará las variables numéricas.

diagnose_numeric(dataset)
diagose_numeric(dataset, variable1, variable2, variable3, …)

diagnose_numeric(dfm)

# A tibble: 36 × 10
   variables   min    Q1   mean median    Q3   max  zero minus outlier
   <chr>     <dbl> <dbl>  <dbl>  <dbl> <dbl> <dbl> <int> <int>   <int>
 1 N             1  61.5 122       122  182.   243     0     0       0
 2 Edad         18  19    20.8      20   22     30     0     0      11
 3 Curso         1   1     1.73      1    2      5     0     0      31
 4 V1            1   3     3.53      4    4      6     0     0      23
 5 V2            1   3     3.30      3    4      6     0     0      15
 6 V3            1   2     3.27      3    4      6     0     0       0
 7 V4            1   3     3.89      4    5      6     0     0       0
 8 V5            1   1     2.70      3    3      6     0     0       0
 9 V6            1   2     3.07      3    4      6     0     0       0
10 V7            1   2     3.25      3    4      6     0     0       0
# ℹ 26 more rows

3.6 Sintaxis para el diagnóstico: variables categóricas

Sólo analizará las variables categóricas

diagnose_category(dataset)
diagnose_category(dataset, variable1, variable2, variable3, …, top=10, type=“rank”) o alternativamente rank=n en lugar de top=n, type=“rank”
- top: número de columnas que serán analizadas (e.g. top=10 incluirá variables de la columan 1 a la 10). Por defecto top=10).
- rank: indica la variable a incluir (e.g. rank=“Estudios”)

diagnose_category(dfm, rank = c(Estudios, Sexo))

# A tibble: 9 × 6
  variables levels     N  freq  ratio  rank
  <chr>     <chr>  <int> <int>  <dbl> <int>
1 Estudios  E        243    83 34.2       1
2 Estudios  C        243    71 29.2       2
3 Estudios  A        243    61 25.1       3
4 Estudios  D        243    23  9.47      4
5 Estudios  B        243     3  1.23      5
6 Estudios  <NA>     243     2  0.823     6
7 Sexo      F        243   213 87.7       1
8 Sexo      M        243    28 11.5       2
9 Sexo      <NA>     243     2  0.823     3

3.7 Sintaxis para el diagnóstico: outliers

diagonse_outliers(dataset)
diagnose_outliers(dataset, variable1, variable2, …)

diagnose_outlier(dfm)

# A tibble: 36 × 6
   variables outliers_cnt outliers_ratio outliers_mean with_mean without_mean
   <chr>            <int>          <dbl>         <dbl>     <dbl>        <dbl>
 1 N                    0           0           NaN       122          122   
 2 Edad                11           4.53         28.5      20.8         20.4 
 3 Curso               31          12.8           4.87      1.73         1.27
 4 V1                  23           9.47          2.30      3.53         3.66
 5 V2                  15           6.17          2         3.30         3.42
 6 V3                   0           0           NaN         3.27         3.27
 7 V4                   0           0           NaN         3.89         3.89
 8 V5                   0           0           NaN         2.70         2.70
 9 V6                   0           0           NaN         3.07         3.07
10 V7                   0           0           NaN         3.25         3.25
# ℹ 26 more rows

3.8 Sintaxis para el diagnóstico: gráfico de outliers

plot_outlier(dfm, Edad, V28) # Se incluyen solamente dos variables como ejemplo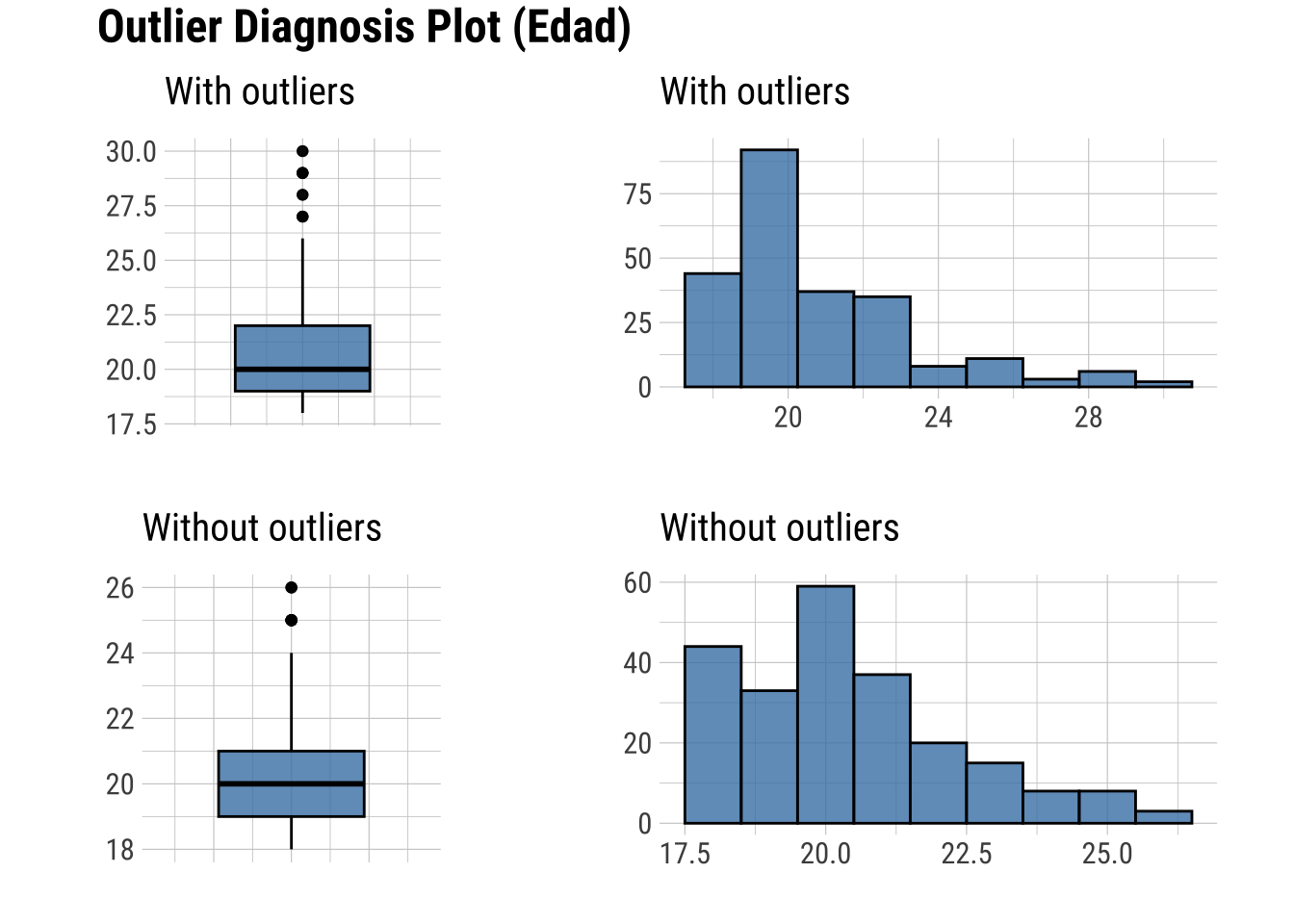

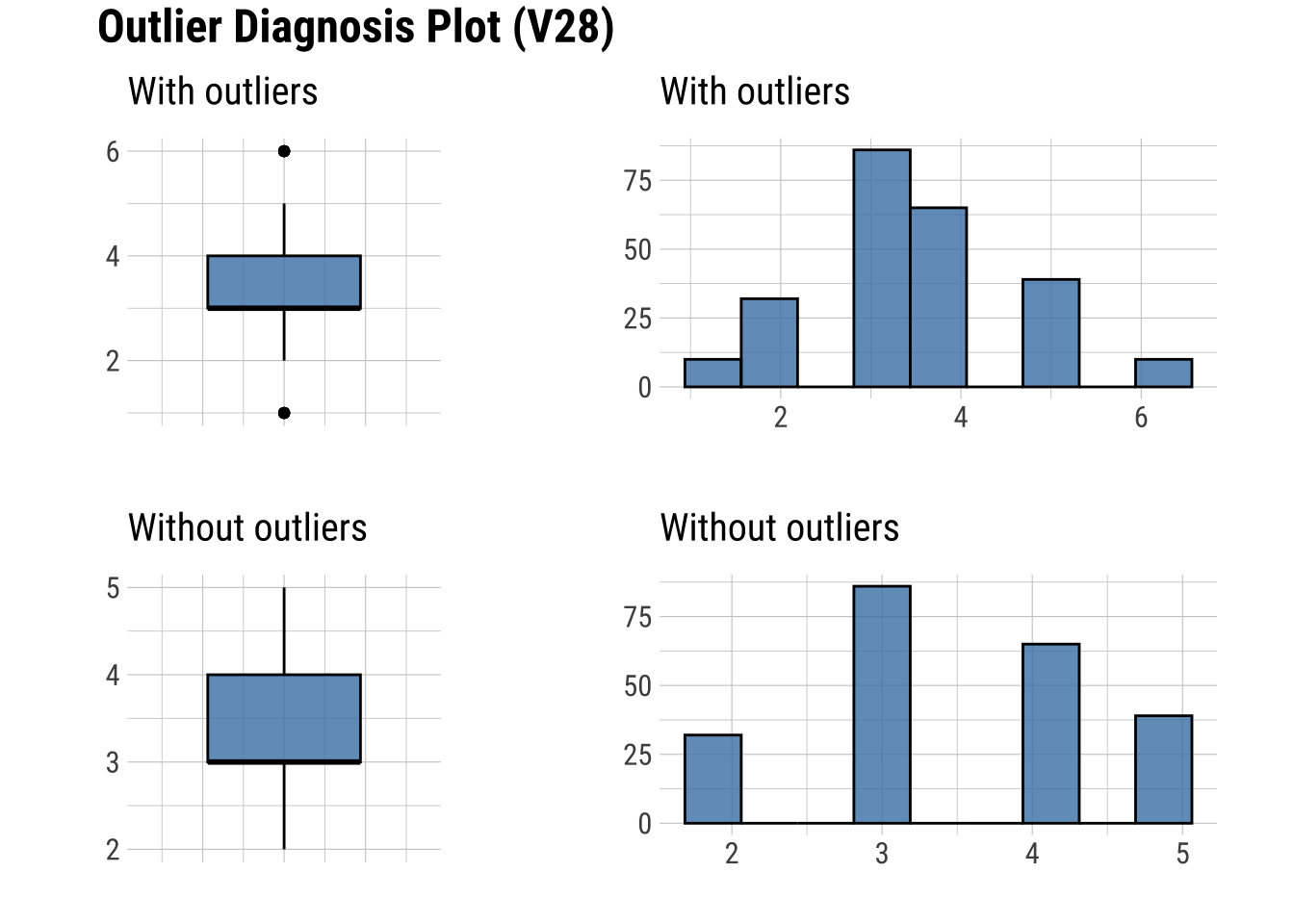
3.9 Sintaxis para el diagnóstico: datos ausentes

find_na(dfm, index = F)

 [1] "Sexo"     "Edad"     "Estudios" "V1"       "V2"       "V3"      
 [7] "V8"       "V9"       "V10"      "V11"      "V12"      "V13"     
[13] "V14"      "V15"      "V16"      "V17"      "V18"      "V19"     
[19] "V20"      "V21"      "V22"      "V23"      "V24"      "V25"     
[25] "V26"      "V27"      "V28"

find_na(dfm, index = F, rate = T) # index=FALSE escribe las variables con NA's; rate=TRUE indica proporción de NA's

          N Universidad        Sexo        Edad    Estudios       Curso 
      0.000       0.000       0.823       2.058       0.823       0.000 
         V1          V2          V3          V4          V5          V6 
      2.469      23.457      13.992       0.000       0.000       0.000 
         V7          V8          V9         V10         V11         V12 
      0.000       0.412       0.412       0.823       1.235       2.058 
        V13         V14         V15         V16         V17         V18 
      2.058       2.469       2.469       2.469       2.469       2.058 
        V19         V20         V21         V22         V23         V24 
      2.058       1.646       1.646       0.823       0.823       0.823 
        V25         V26         V27         V28         V29         V30 
      0.412       0.412       0.412       0.412       0.000       0.000 
        V31         V32         V33 
      0.000       0.000       0.000

3.10 Sintaxis para el diagnóstico: datos ausentes usando dplyr

diagnose(dfm) |>
  filter(missing_count > 0)

# A tibble: 27 × 6
   variables types     missing_count missing_percent unique_count unique_rate
   <chr>     <chr>             <int>           <dbl>        <int>       <dbl>
 1 Sexo      character             2           0.823            3      0.0123
 2 Edad      numeric               5           2.06            14      0.0576
 3 Estudios  character             2           0.823            6      0.0247
 4 V1        numeric               6           2.47             7      0.0288
 5 V2        numeric              57          23.5              7      0.0288
 6 V3        numeric              34          14.0              7      0.0288
 7 V8        numeric               1           0.412            7      0.0288
 8 V9        numeric               1           0.412            7      0.0288
 9 V10       numeric               2           0.823            7      0.0288
10 V11       numeric               3           1.23             7      0.0288
# ℹ 17 more rows

3.11 Sintaxis para el diagnóstico: gráfico de intersección de ausentes

plot_na_intersect(dfm) # : visualiza las combinaciones de valores faltantes entre columnas.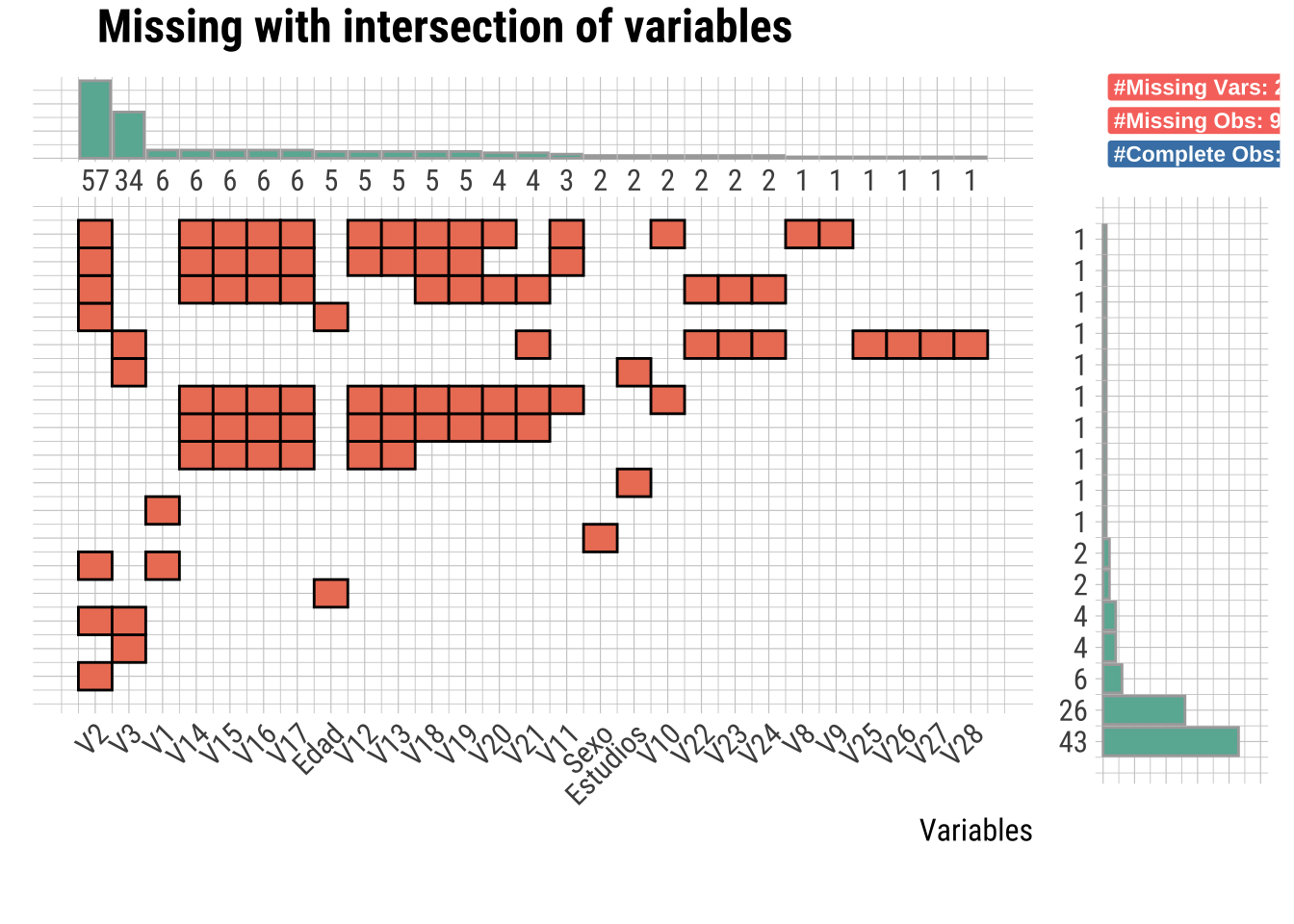

plot_na_pareto(dfm, only_na = T, plot = T) # Si plot=F obtenemos la tabla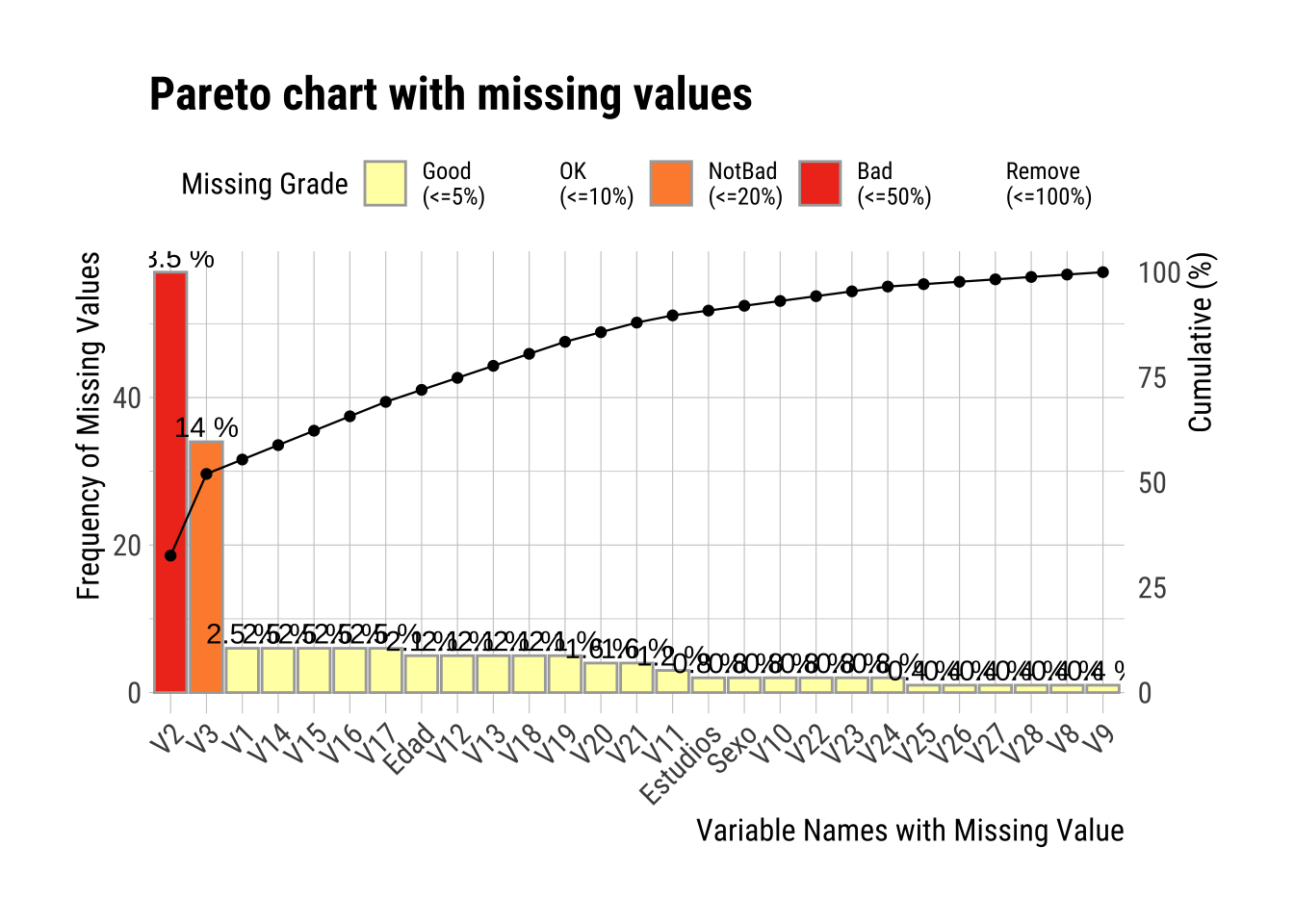

3.12 Sintaxis para tener salidas más agradables

diagnose(dfm, 2:10) %>% flextable() # Como ejemplo, sólo se han hecho con las variables desde la columna 2 a la 10

variables	types	missing_count	missing_percent	unique_count	unique_rate
Universidad	character	0	0.0000000	3	0.01234568
Sexo	character	2	0.8230453	3	0.01234568
Edad	numeric	5	2.0576132	14	0.05761317
Estudios	character	2	0.8230453	6	0.02469136
Curso	numeric	0	0.0000000	5	0.02057613
V1	numeric	6	2.4691358	7	0.02880658
V2	numeric	57	23.4567901	7	0.02880658
V3	numeric	34	13.9917695	7	0.02880658
V4	numeric	0	0.0000000	6	0.02469136

4 Reparar

Al reparar, principalmente trataremos de solucionar lo siguiente:

Los datos ausentes (NA).
Los datos extremos (outliers).

Las dos estrategias básicas son:

Eliminación de casos (a veces la consideración de no tener en cuenta la variable).
Imputación de valores.

También veremos como agrupar valores (binning).

4.1 Casos NA

4.1.1 Casos con problemas en el dataset ejemplo

En el diagnóstico anterior, las variables con un elevado número de NA’s eran las siguientes:

Edad: 2.058
V1: 2.469
V2: 23.457
V3: 13.992
V13: 2.058
V14: 2.469
V15: 2.469
V16: 2.469
V17: 2.469
V18: 2.058
V19: 2.058

4.1.2 Gestionar NA’s: eliminar

El paquete dlookr no tiene una función definida para eliminar casos. Se puede recurrir a otros paquetes (e.g. dplyr).

dfm_sin_na <- dfm %>%
  filter(complete.cases(.))

nrow(dfm) - nrow(dfm_sin_na) # Comprobamos cuantos casos se han eliminado

4.1.3 Gestionar NA’s en el dataset de ejemplo: eliminación

Eliminación casos

Los casos con más de 5 NA’s los eliminaremos porque sospechamos que son sujetos que no son “de fiar”.
También se quitarán los casos sin el Sexo declarado por las implicaciones que puede llevar a la hora de analizar los datos. Esto depende del objetivo/s de investigación.

# Contar los NA por fila y eliminar las que tienen 5 o más NA's
dfm_filtrado <- dfm %>%
  filter(!is.na(Sexo)) %>%
  mutate(na_count = rowSums(is.na(.))) %>%
  filter(na_count < 5) %>%
  select(-na_count) # Eliminar la columna auxiliar

Buscasmos las variables que quedan con NA’s. A las que quedan, se les realizará la imputación.

find_na(dfm_filtrado, index = F)

[1] "Edad"     "Estudios" "V1"       "V2"       "V3"

diagnose(dfm_filtrado, Edad, Estudios, V1, V2, V3)

# A tibble: 5 × 6
  variables types     missing_count missing_percent unique_count unique_rate
  <chr>     <chr>             <int>           <dbl>        <int>       <dbl>
1 Edad      numeric               5           2.14            14      0.0598
2 Estudios  character             2           0.855            6      0.0256
3 V1        numeric               6           2.56             7      0.0299
4 V2        numeric              54          23.1              7      0.0299
5 V3        numeric              33          14.1              7      0.0299

4.1.4 Gestionar NA’s: imputación

Método	Tipo de variable	¿Qué hace?	Pros	Contras
Media (`mean`)	Numérica	Sustituye los valores perdidos por la media aritmética de la variable.	- Simple y rápido - Útil si la distribución es simétrica	- Afectado por outliers - Reduce la variabilidad del conjunto
Mediana (`median`)	Numérica	Sustituye los NA por la mediana (valor central) de la variable.	- Robusta frente a valores extremos - Ideal para datos asimétricos	- Puede crear empates artificiales
Moda (`mode`)	Numérica o Categórica	Rellena los NA con el valor más frecuente en la variable.	- Usa el valor más común - Mantiene coherencia con los datos	- No siempre hay una moda clara - Puede sobrerrepresentar una clase

4.1.5 Gestionar NA’s: imputación

Se puede hacer un gráfico para ver qué procedimiento se ajusta mejor. Hay que tener en cuenta otros factores (metodológicos) en cuenta.

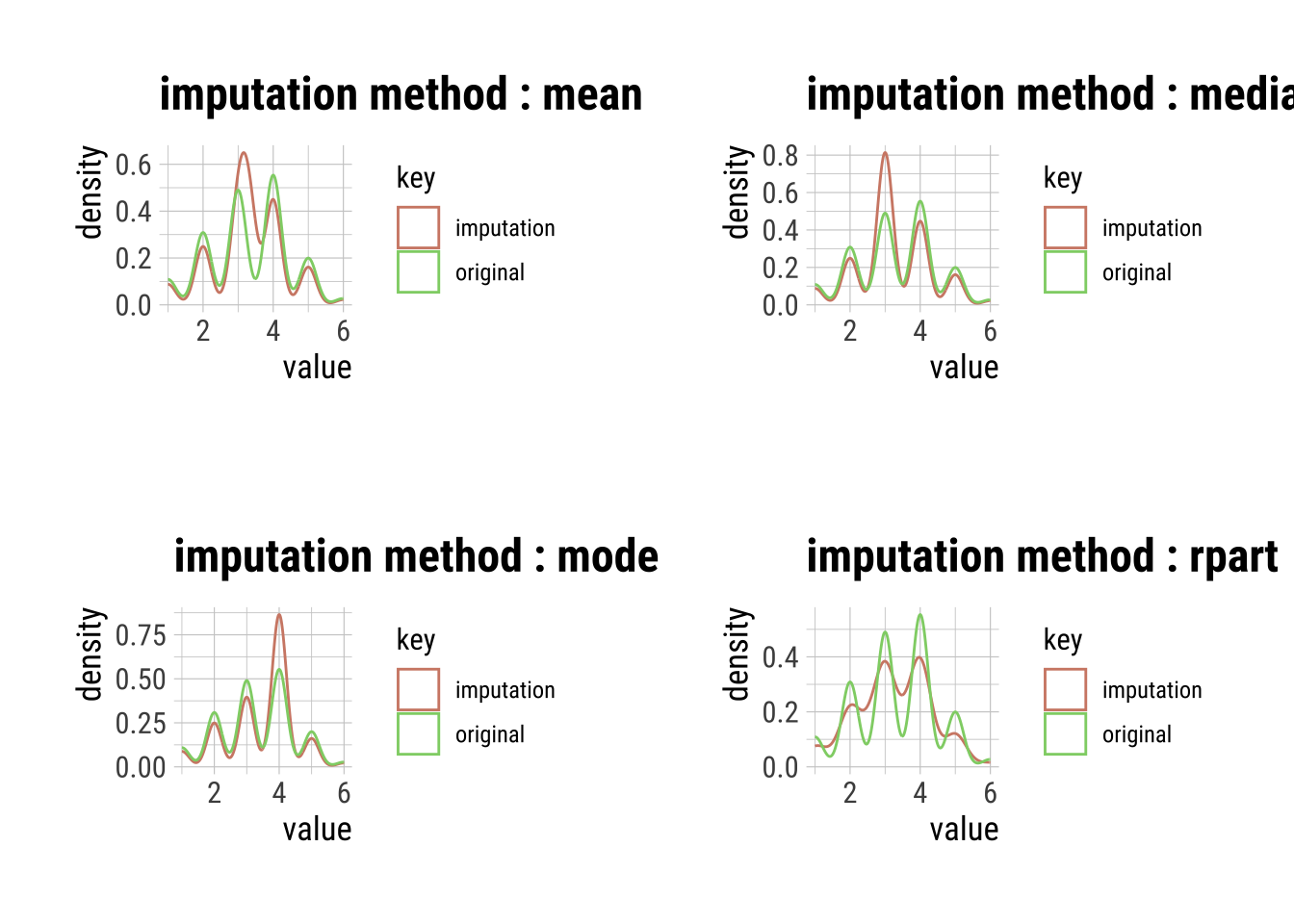
4.1.6 Gestionar NA’s en el dataset de ejemplo: imputación

Imputamos valores utilizando el método que consideramos más adecuado.

# Variable Edad (escalar)
# Media
Edad_imp <- imputate_na(dfm_filtrado, Edad, method = "mean")
summary(Edad_imp)

Impute missing values with mean

* Information of Imputation (before vs after)
                    Original    Imputation 
described_variables "value"     "value"    
n                   "229"       "234"      
na                  "5"         "0"        
mean                "20.80786"  "20.80786" 
sd                  "2.596849"  "2.568834" 
se_mean             "0.1716046" "0.1679299"
IQR                 "3"         "3"        
skewness            "1.388083"  "1.402956" 
kurtosis            "2.009120"  "2.117795" 
p00                 "18"        "18"       
p01                 "18"        "18"       
p05                 "18"        "18"       
p10                 "18"        "18"       
p20                 "19"        "19"       
p25                 "19"        "19"       
p30                 "19"        "19"       
p40                 "20"        "20"       
p50                 "20"        "20"       
p60                 "21"        "21"       
p70                 "21"        "21"       
p75                 "22"        "22"       
p80                 "22"        "22"       
p90                 "24"        "24"       
p95                 "26"        "26"       
p99                 "29"        "29"       
p100                "30"        "30"

plot(Edad_imp)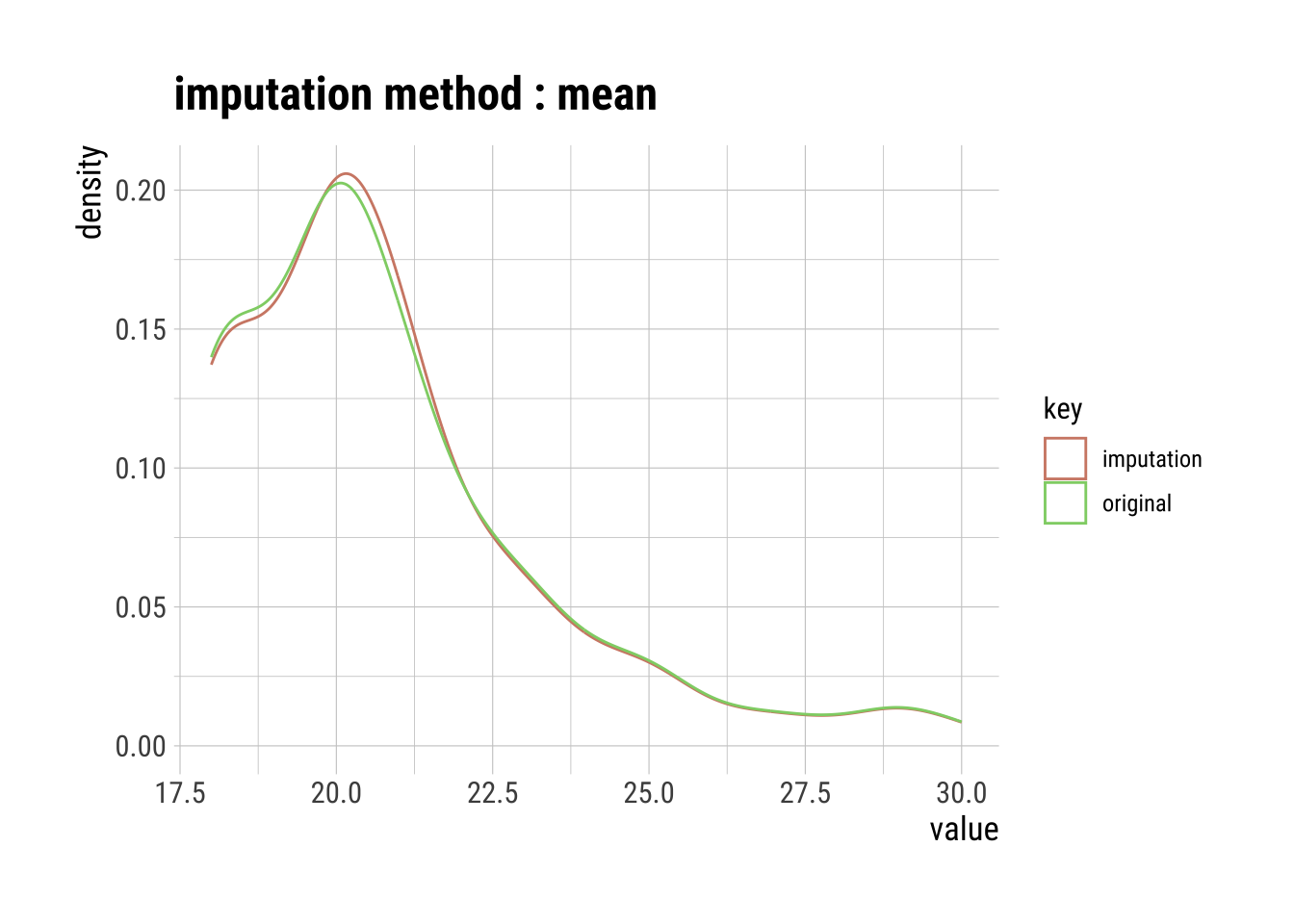

# Variable Estudios (categórica)
# Moda
## En el caso de la variable Estudios, es necesario recodificarla como números
dfm_filtrado <- dfm_filtrado %>%
  mutate(Estudios_num = case_when(
    Estudios == "A" ~ 1,
    Estudios == "B" ~ 2,
    Estudios == "C" ~ 3,
    Estudios == "D" ~ 4,
    Estudios == "E" ~ 5
  ))

Estudios_imp <- imputate_na(dfm_filtrado, Estudios_num, method = "mode")
summary(Estudios_imp)

Impute missing values with mode

* Information of Imputation (before vs after)
                    Original     Imputation  
described_variables "value"      "value"     
n                   "232"        "234"       
na                  "2"          "0"         
mean                "3.241379"   "3.256410"  
sd                  "1.552101"   "1.553917"  
se_mean             "0.1019004"  "0.1015827" 
IQR                 "4.00"       "3.75"      
skewness            "-0.2828929" "-0.2961816"
kurtosis            "-1.324040"  "-1.321206" 
p00                 "1"          "1"         
p01                 "1"          "1"         
p05                 "1"          "1"         
p10                 "1"          "1"         
p20                 "1"          "1"         
p25                 "1.00"       "1.25"      
p30                 "3"          "3"         
p40                 "3"          "3"         
p50                 "3"          "3"         
p60                 "4"          "4"         
p70                 "5"          "5"         
p75                 "5"          "5"         
p80                 "5"          "5"         
p90                 "5"          "5"         
p95                 "5"          "5"         
p99                 "5"          "5"         
p100                "5"          "5"

plot(Estudios_imp)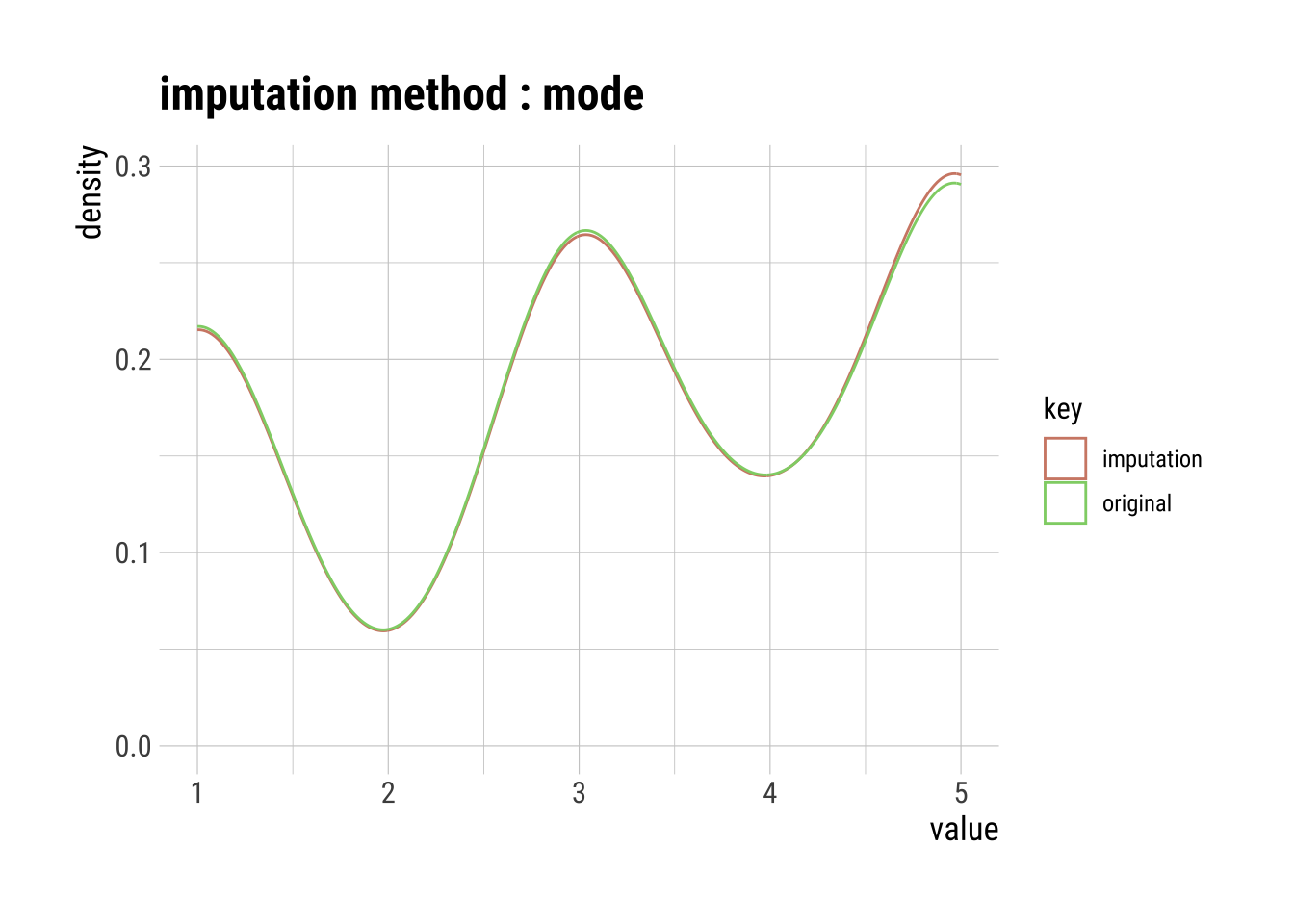

# Mediana (ordinal)
V1_imp <- imputate_na(dfm_filtrado, V1, method = "median")
summary(V1_imp)

Impute missing values with median

* Information of Imputation (before vs after)
                    Original      Imputation   
described_variables "value"       "value"      
n                   "228"         "234"        
na                  "6"           "0"          
mean                "3.517544"    "3.529915"   
sd                  "1.155202"    "1.142790"   
se_mean             "0.07650515"  "0.07470650" 
IQR                 "1"           "1"          
skewness            "-0.3630838"  "-0.3961052" 
kurtosis            "-0.14065968" "-0.07398022"
p00                 "1"           "1"          
p01                 "1"           "1"          
p05                 "1"           "1"          
p10                 "2"           "2"          
p20                 "3"           "3"          
p25                 "3"           "3"          
p30                 "3"           "3"          
p40                 "3"           "3"          
p50                 "4"           "4"          
p60                 "4"           "4"          
p70                 "4"           "4"          
p75                 "4"           "4"          
p80                 "4"           "4"          
p90                 "5"           "5"          
p95                 "5"           "5"          
p99                 "6"           "6"          
p100                "6"           "6"

plot(V1_imp)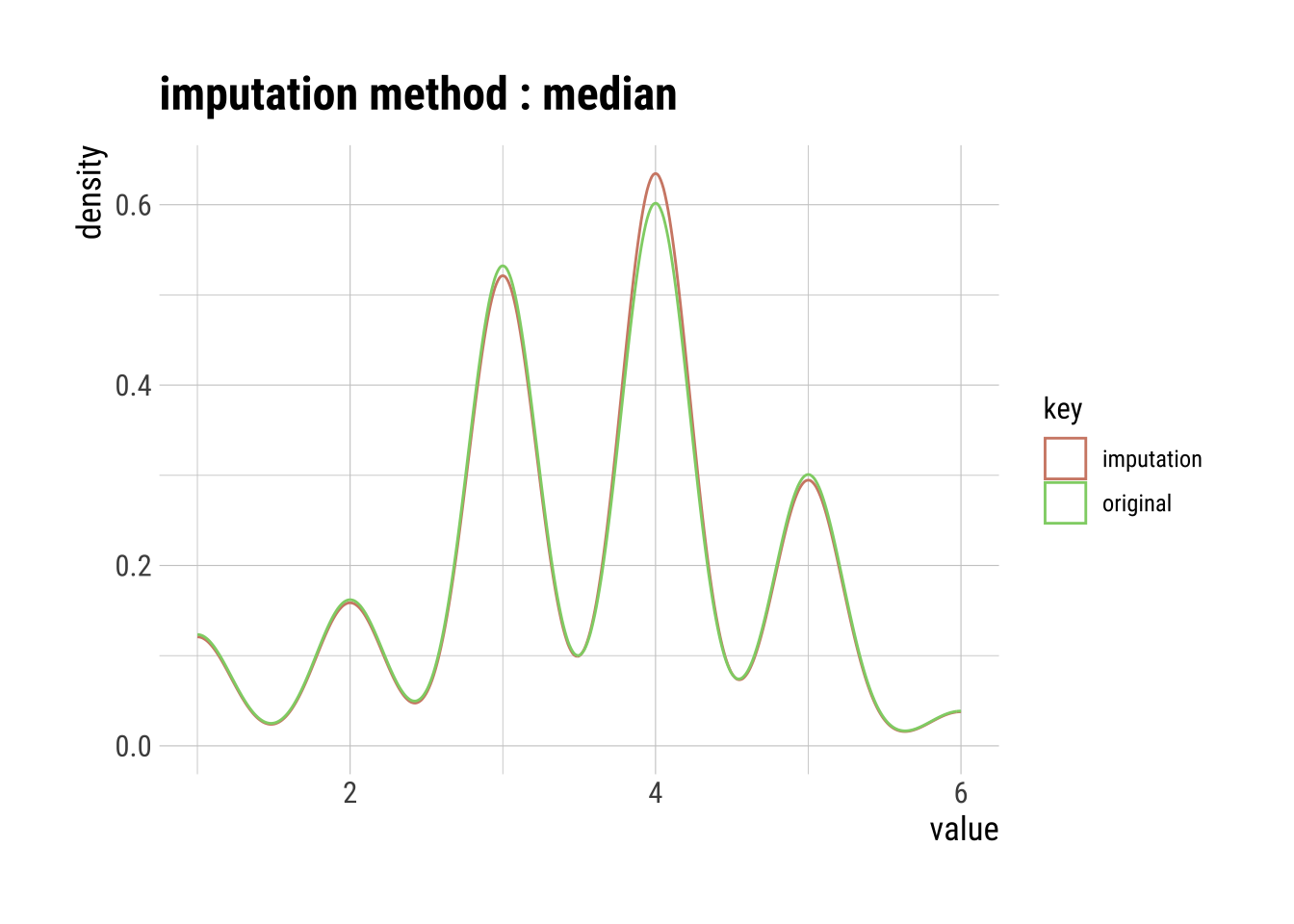

4.1.6.1 Ojo, ¿qué pasa con variables con elevadas NA’s?

Nos paramos con las variables con altos NA’s. Teniendo en cuenta que son categóricas (medida ordinal).

Variable 2

# Variable V2

# Partición recursiva y árboles de regresión
V2_imp_Mo <- imputate_na(dfm_filtrado, V2, method = "mode")
V2_imp_Md <- imputate_na(dfm_filtrado, V2, method = "median")
V2_imp_Mc <- imputate_na(dfm_filtrado, V2, method = "mice", seed = 1234)


 iter imp variable
  1   1  Edad  V1  V2  V3  Estudios_num
  1   2  Edad  V1  V2  V3  Estudios_num
  1   3  Edad  V1  V2  V3  Estudios_num
  1   4  Edad  V1  V2  V3  Estudios_num
  1   5  Edad  V1  V2  V3  Estudios_num
  2   1  Edad  V1  V2  V3  Estudios_num
  2   2  Edad  V1  V2  V3  Estudios_num
  2   3  Edad  V1  V2  V3  Estudios_num
  2   4  Edad  V1  V2  V3  Estudios_num
  2   5  Edad  V1  V2  V3  Estudios_num
  3   1  Edad  V1  V2  V3  Estudios_num
  3   2  Edad  V1  V2  V3  Estudios_num
  3   3  Edad  V1  V2  V3  Estudios_num
  3   4  Edad  V1  V2  V3  Estudios_num
  3   5  Edad  V1  V2  V3  Estudios_num
  4   1  Edad  V1  V2  V3  Estudios_num
  4   2  Edad  V1  V2  V3  Estudios_num
  4   3  Edad  V1  V2  V3  Estudios_num
  4   4  Edad  V1  V2  V3  Estudios_num
  4   5  Edad  V1  V2  V3  Estudios_num
  5   1  Edad  V1  V2  V3  Estudios_num
  5   2  Edad  V1  V2  V3  Estudios_num
  5   3  Edad  V1  V2  V3  Estudios_num
  5   4  Edad  V1  V2  V3  Estudios_num
  5   5  Edad  V1  V2  V3  Estudios_num

Warning: Number of logged events: 3

V2_imp_R <- imputate_na(dfm_filtrado, V2, method = "rpart")

# par(mfrow = c(2, 2))
p1 <- plot(V2_imp_Mo)
p2 <- plot(V2_imp_Md)
p3 <- plot(V2_imp_Mc)
p4 <- plot(V2_imp_R)
grid.arrange(p1, p2, p3, p4, ncol = 2)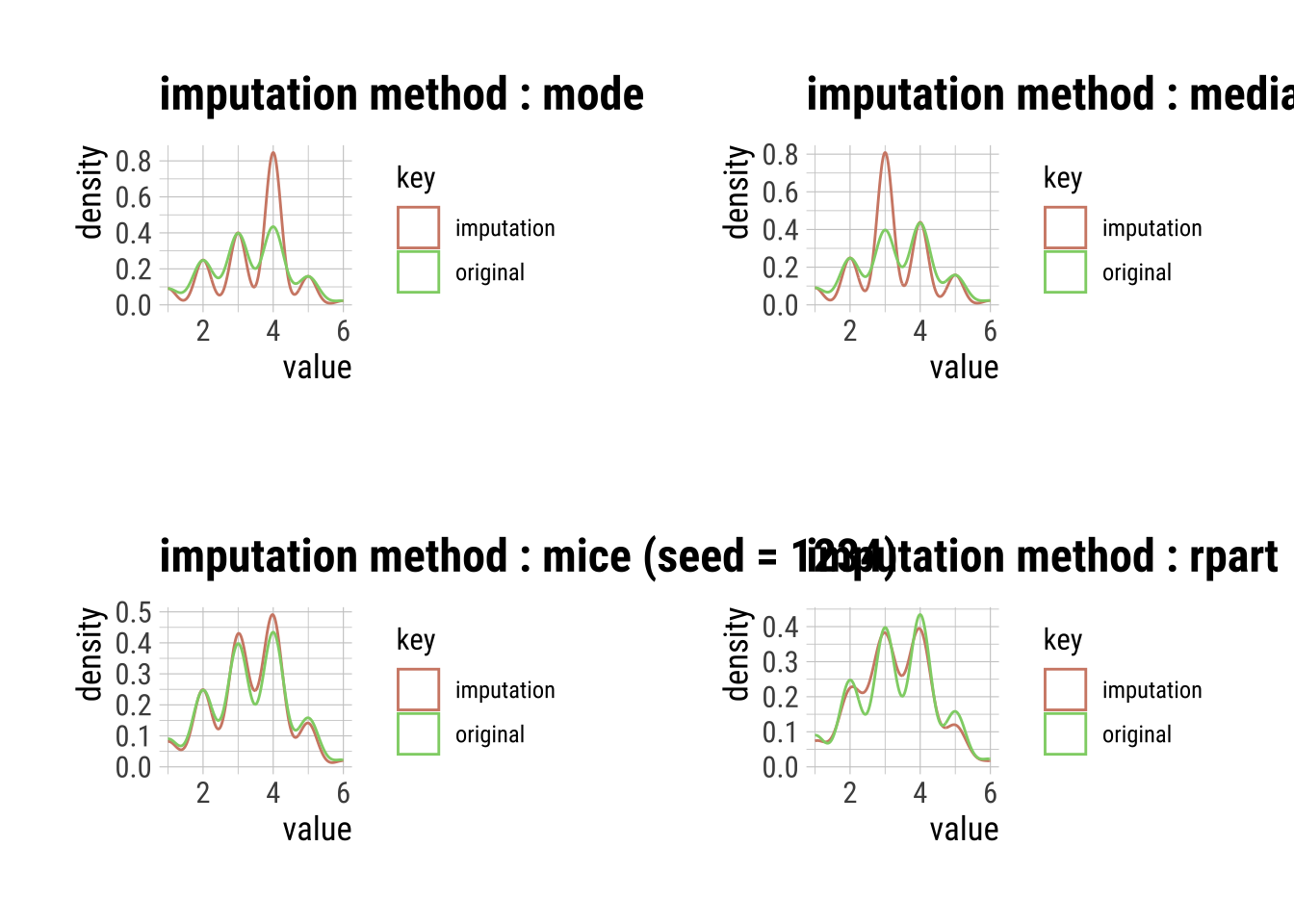

Variable 3

# Variable V3

# Partición recursiva y árboles de regresión
V3_imp_Mo <- imputate_na(dfm_filtrado, V3, method = "mode")
V3_imp_Md <- imputate_na(dfm_filtrado, V3, method = "median")
V3_imp_Mc <- imputate_na(dfm_filtrado, V3, method = "mice", seed = 1234)


 iter imp variable
  1   1  Edad  V1  V2  V3  Estudios_num
  1   2  Edad  V1  V2  V3  Estudios_num
  1   3  Edad  V1  V2  V3  Estudios_num
  1   4  Edad  V1  V2  V3  Estudios_num
  1   5  Edad  V1  V2  V3  Estudios_num
  2   1  Edad  V1  V2  V3  Estudios_num
  2   2  Edad  V1  V2  V3  Estudios_num
  2   3  Edad  V1  V2  V3  Estudios_num
  2   4  Edad  V1  V2  V3  Estudios_num
  2   5  Edad  V1  V2  V3  Estudios_num
  3   1  Edad  V1  V2  V3  Estudios_num
  3   2  Edad  V1  V2  V3  Estudios_num
  3   3  Edad  V1  V2  V3  Estudios_num
  3   4  Edad  V1  V2  V3  Estudios_num
  3   5  Edad  V1  V2  V3  Estudios_num
  4   1  Edad  V1  V2  V3  Estudios_num
  4   2  Edad  V1  V2  V3  Estudios_num
  4   3  Edad  V1  V2  V3  Estudios_num
  4   4  Edad  V1  V2  V3  Estudios_num
  4   5  Edad  V1  V2  V3  Estudios_num
  5   1  Edad  V1  V2  V3  Estudios_num
  5   2  Edad  V1  V2  V3  Estudios_num
  5   3  Edad  V1  V2  V3  Estudios_num
  5   4  Edad  V1  V2  V3  Estudios_num
  5   5  Edad  V1  V2  V3  Estudios_num

Warning: Number of logged events: 3

V3_imp_R <- imputate_na(dfm_filtrado, V3, method = "rpart")

# par(mfrow = c(2, 2))
p1 <- plot(V3_imp_Mo)
p2 <- plot(V3_imp_Md)
p3 <- plot(V3_imp_Mc)
p4 <- plot(V3_imp_R)
grid.arrange(p1, p2, p3, p4, ncol = 2)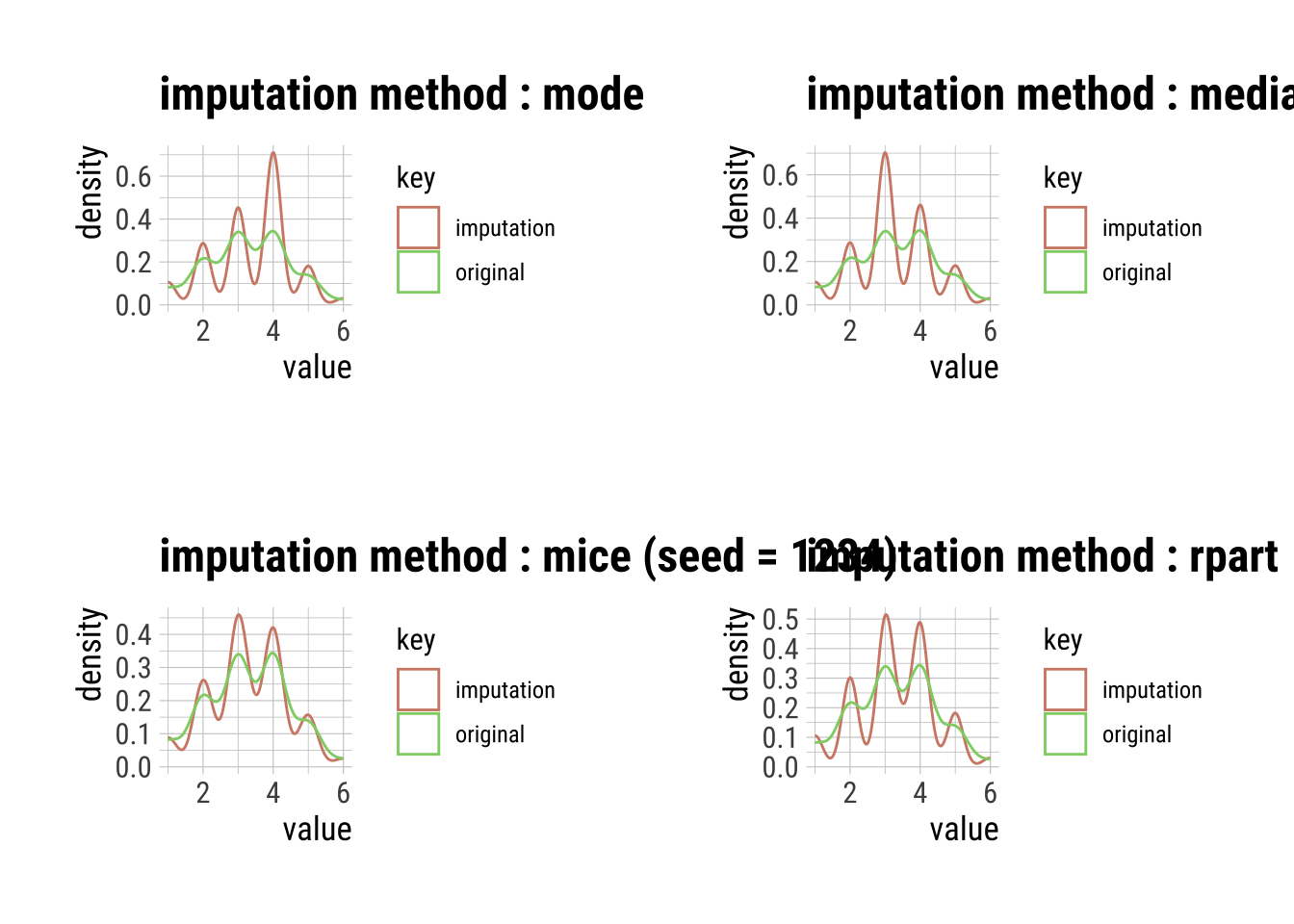

4.1.7 Crear dataset nuevo (provisional)

Una vez con las variables imputadas, nos “apañamos” un dataset temporal que recoga los casos sin NA’s que llevamos hasta el momento:

dfm_filtrado$Edad_imp <- Edad_imp
dfm_filtrado$Estudios_imp <- Estudios_imp
dfm_filtrado$V1_imp <- V1_imp
dfm_filtrado$V2_imp <- V2_imp_Mc
dfm_filtrado$V3_imp <- V3_imp_Mc
dim(dfm_filtrado)

[1] 234  45

4.2 Outliers

4.2.1 Encontrar variables con outliers

find_outliers(dfm_filtrado, index = F)

 [1] "Edad"  "Curso" "V1"    "V8"    "V14"   "V16"   "V18"   "V19"   "V20"  
[10] "V22"   "V25"   "V28"

De las que aparecen, no nos interesan Edad (porque trabajamos ya con Edad_imp), Curso (porque la muestra estaba ya sesgada desde origen), ni V1 (porque trabajamos ya con V1_imp)

Realizamos un nuevo diagnóstico para valorar qué variables se deberían transformar, en función de criterios dirigidos por el objetivo de investigación (e.g. por diferencias grandes en los promedios).

dagnos <- diagnose_outlier(dfm_filtrado, V8, V14, V16, V18, V19, V20, V22, V25, V28)
dife <- dagnos$with_mean - dagnos$without_mean
tabla <- cbind(dagnos, dife)
tabla

  variables outliers_cnt outliers_ratio outliers_mean with_mean without_mean
1        V8           21       8.974359      1.952381  3.354701     3.492958
2       V14           30      12.820513      2.166667  3.435897     3.622549
3       V16           25      10.683761      3.000000  3.427350     3.478469
4       V18           28      11.965812      2.964286  3.222222     3.257282
5       V19           14       5.982906      5.285714  2.790598     2.631818
6       V20           15       6.410256      5.266667  2.705128     2.529680
7       V22           14       5.982906      5.285714  2.799145     2.640909
8       V25           22       9.401709      5.500000  2.683761     2.391509
9       V28           20       8.547009      3.500000  3.529915     3.532710
         dife
1 -0.13825689
2 -0.18665158
3 -0.05111847
4 -0.03505933
5  0.15878011
6  0.17544784
7  0.15823621
8  0.29225125
9 -0.00279575

plot_outlier(dfm_filtrado, V8, V14, V16, V18, V19, V20, V22, V25, V28)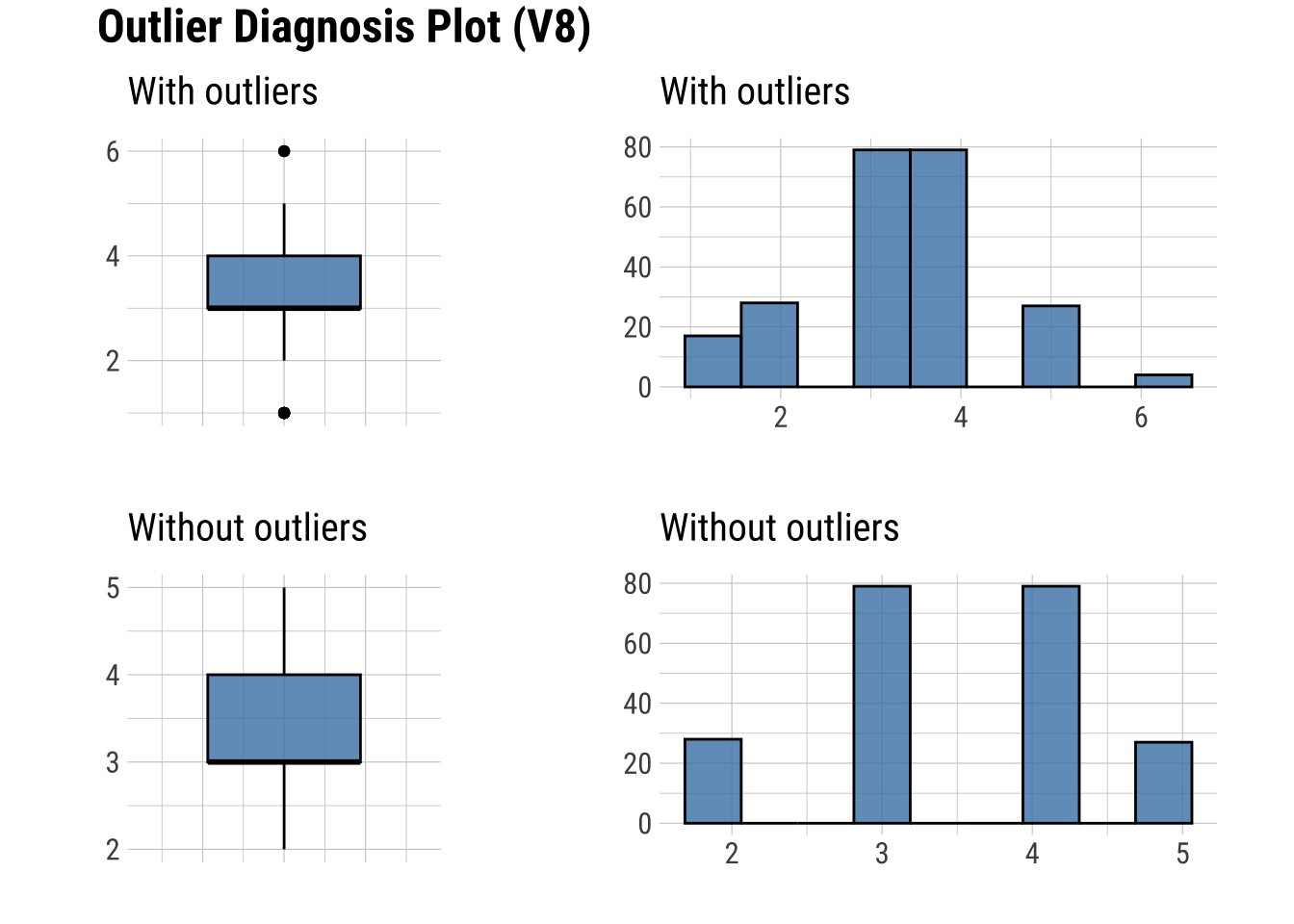

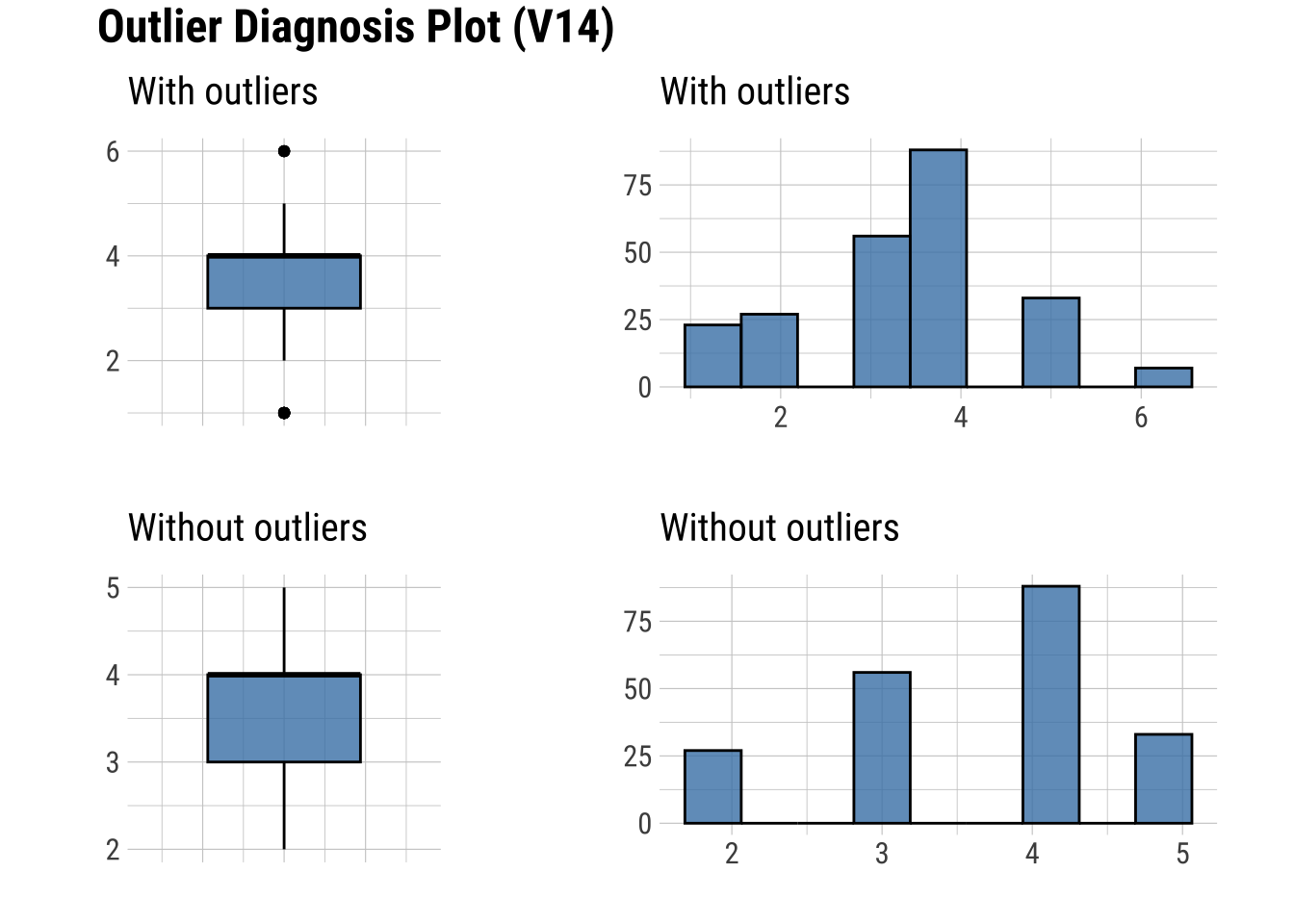
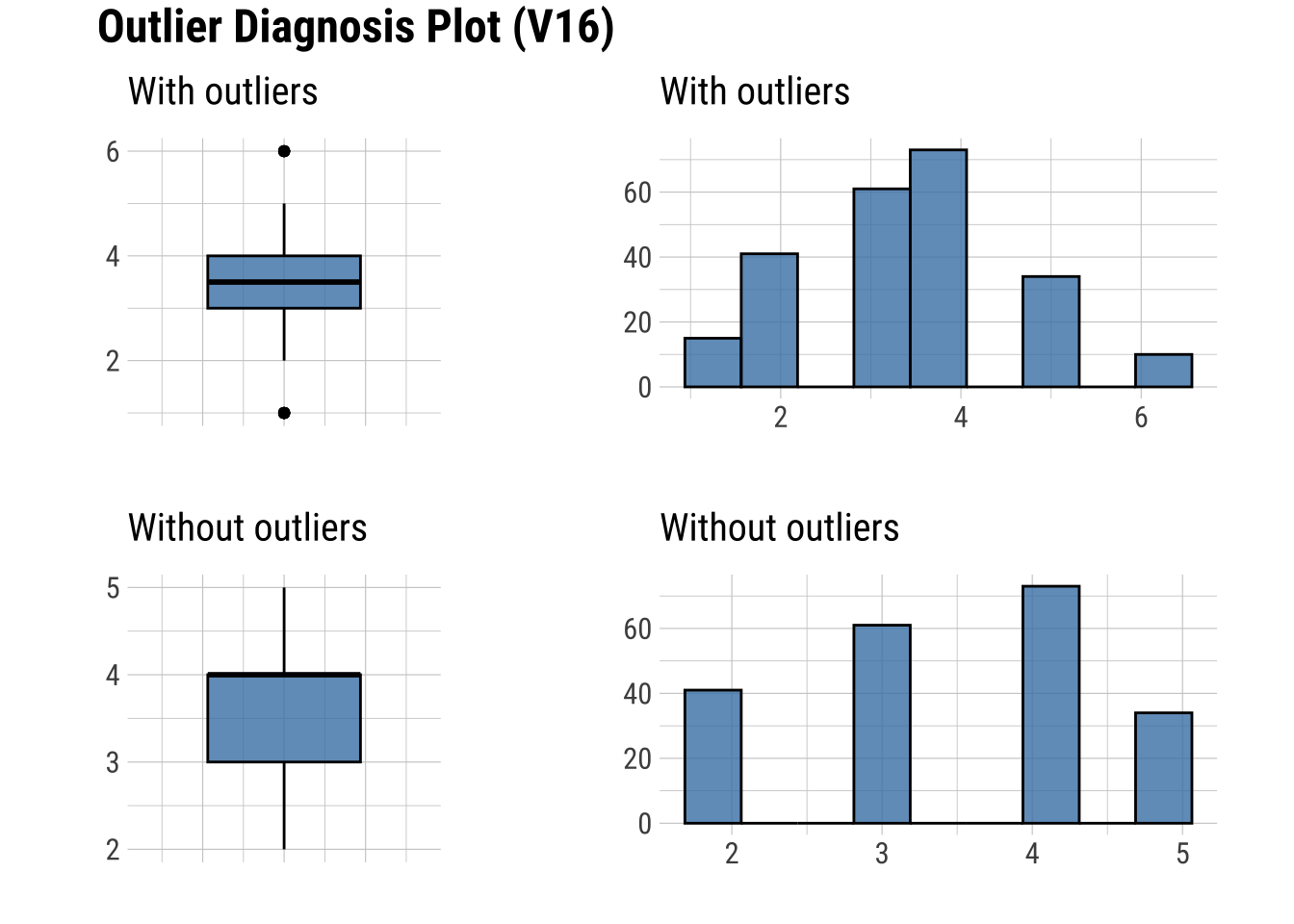
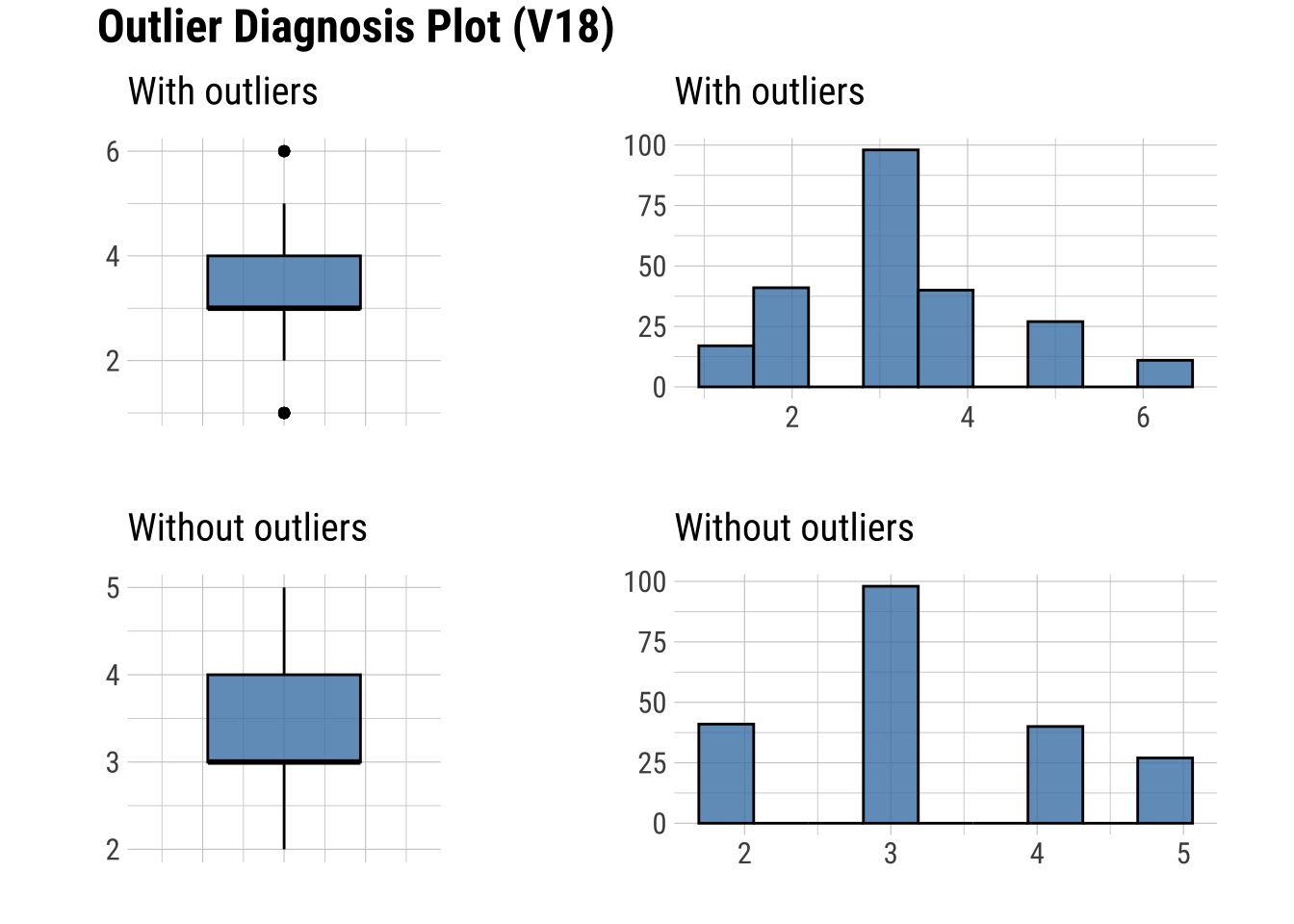
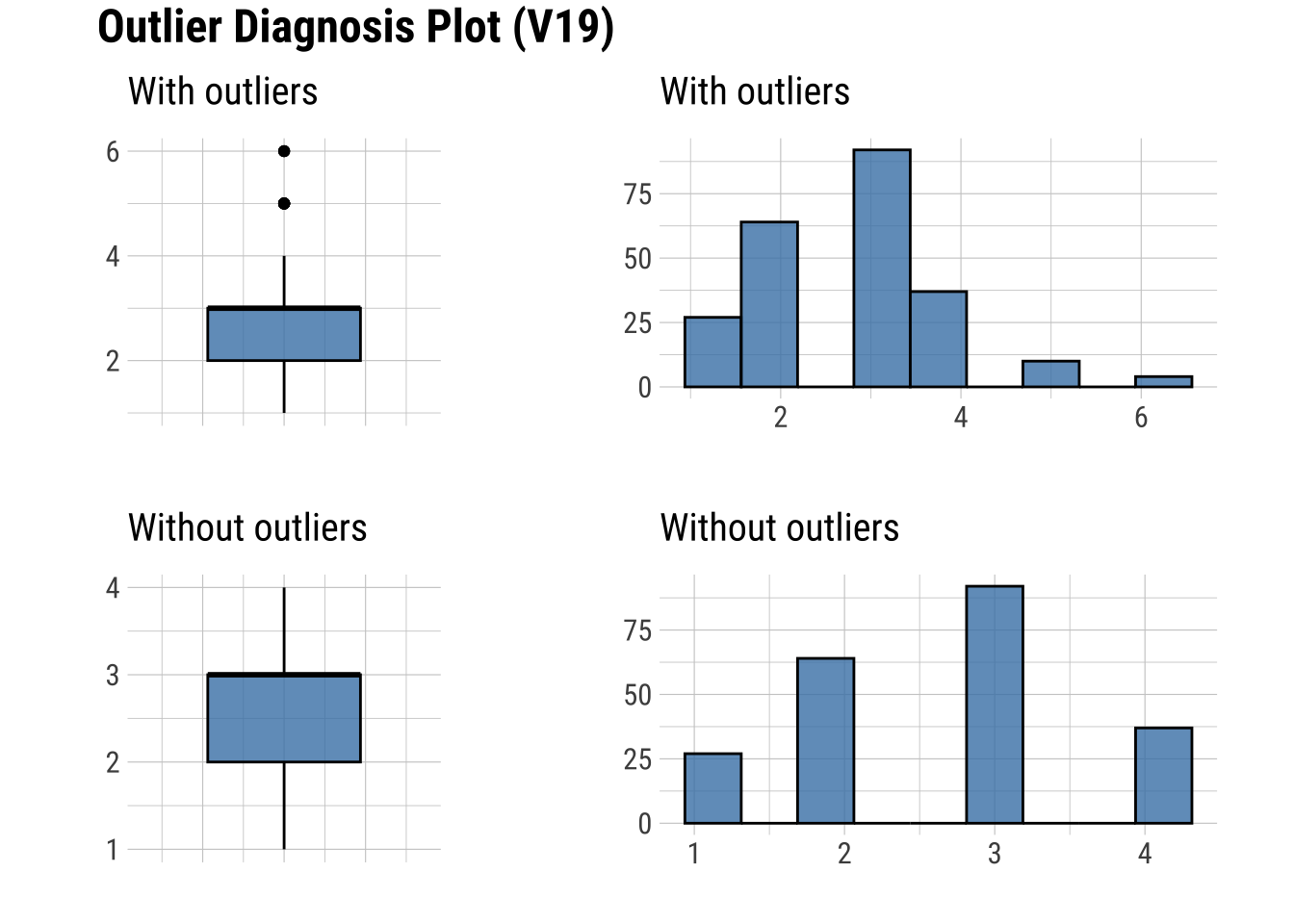
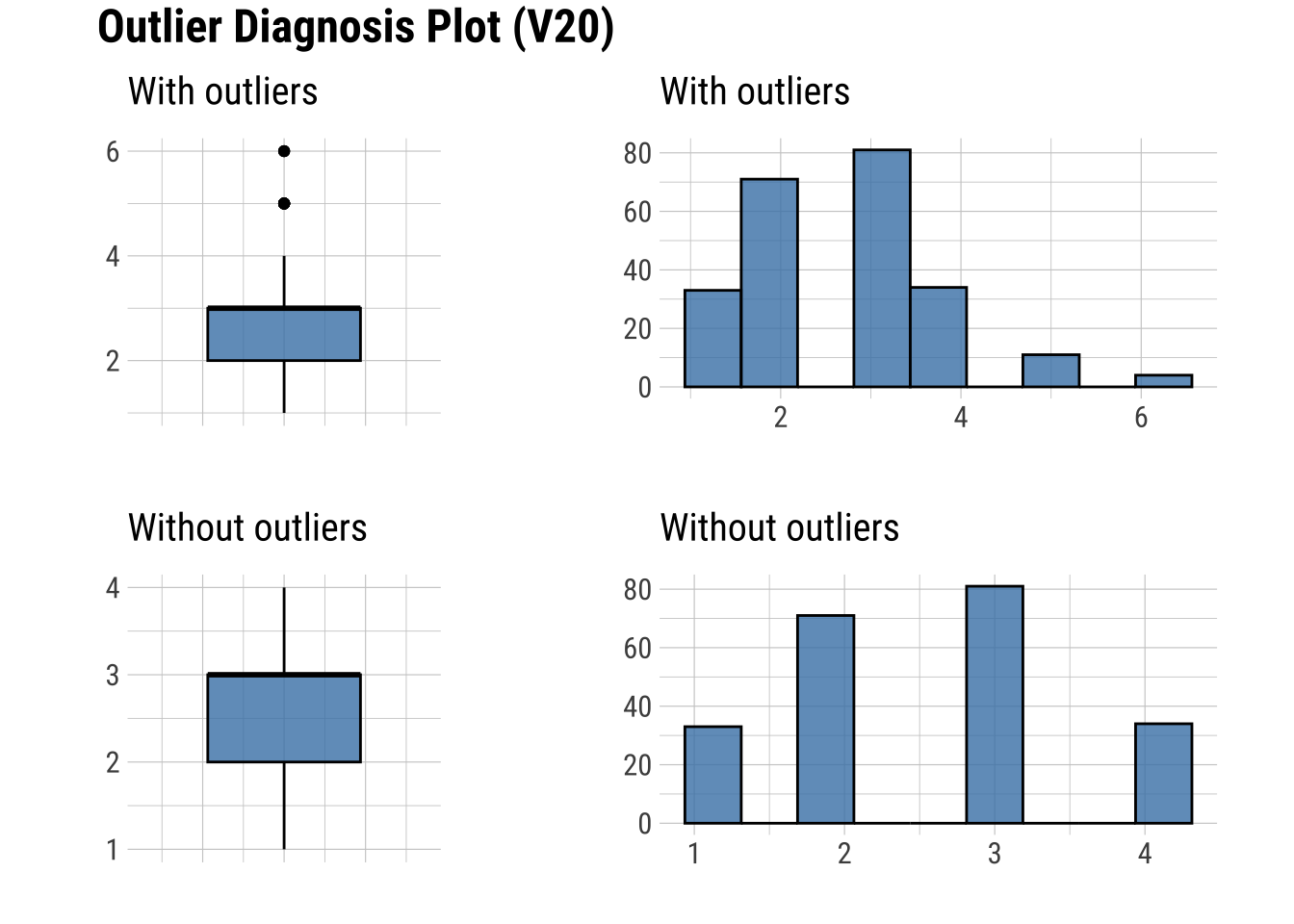
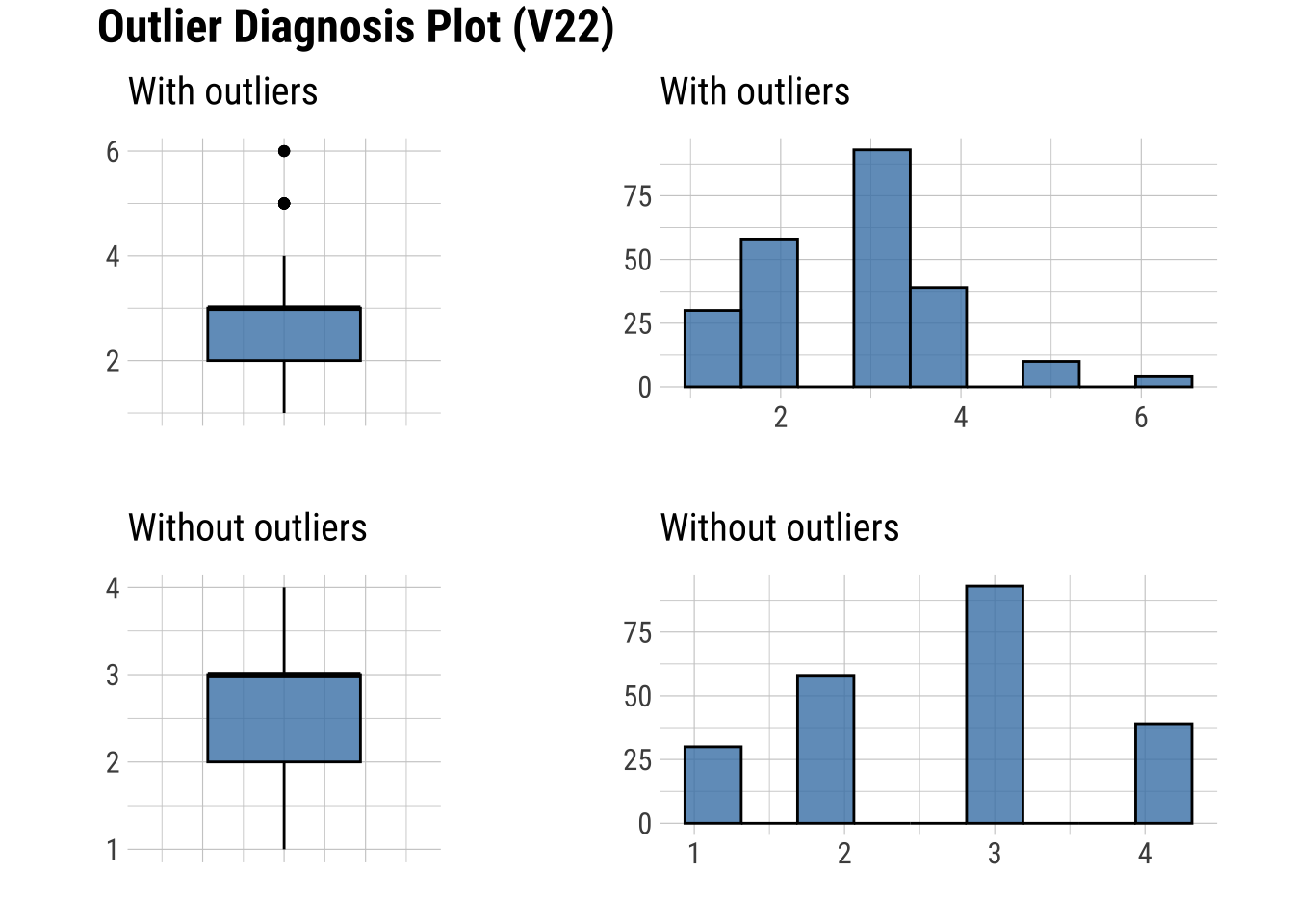
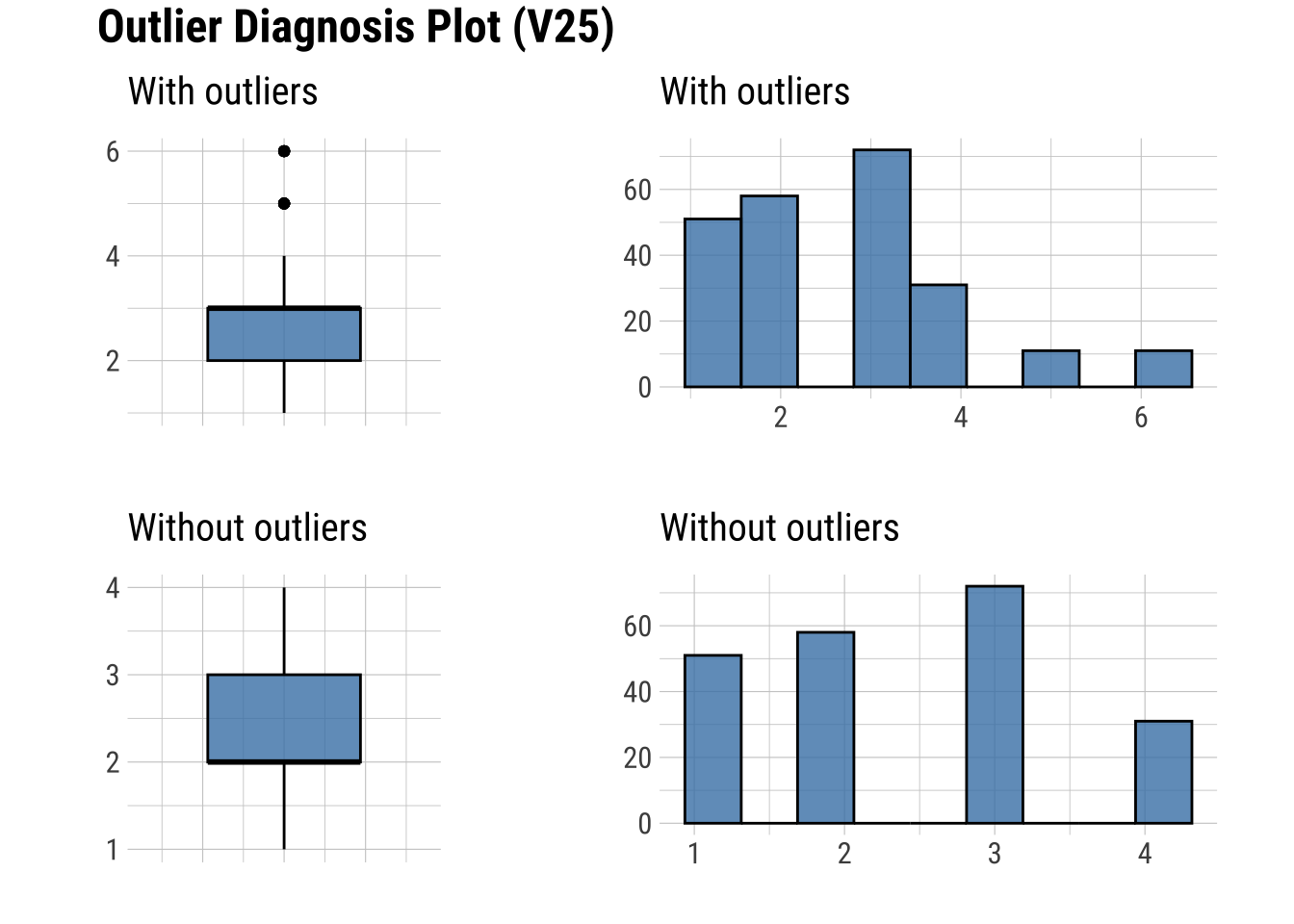
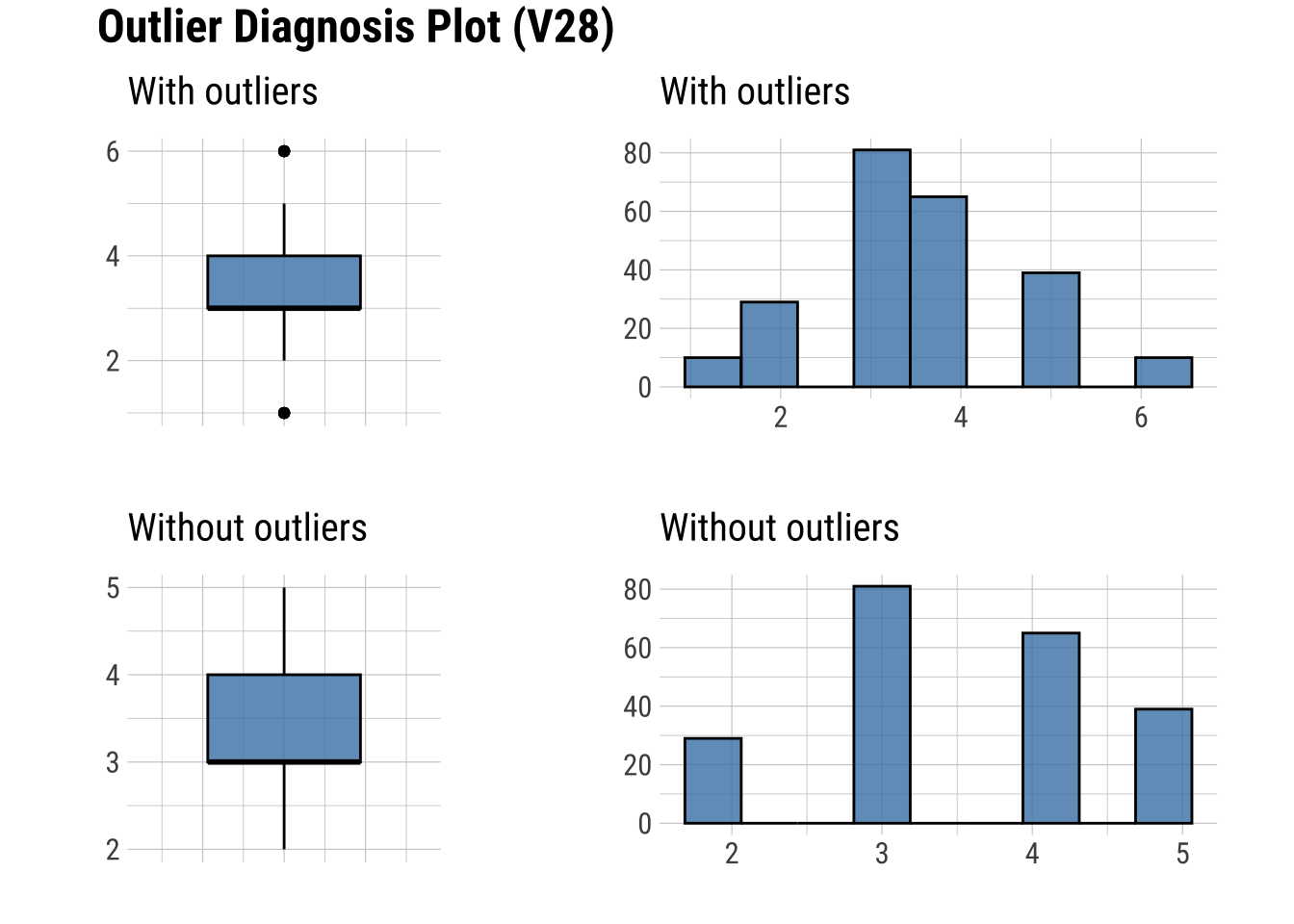
Se observan cambios destacados en V25.

4.2.2 Gestionar outliers: eliminar casos

Una posibilidad es eliminarlos.
Se va a realizar sólo como ejemplo,
sin embargo, en los datos finales no se realizará porque el % de eliminación alcanzaría casi el 10% de los casos (ver tabla de diagnóstico de outliers)

Lo hacemos con la variable V8 como ejemplo.

Q1 <- quantile(dfm_filtrado$V8, .25)
Q3 <- quantile(dfm_filtrado$V8, .75)
IQR <- IQR(dfm_filtrado$V8)
no_outliers <- subset(dfm_filtrado, dfm_filtrado$V8 > (Q1 - 1.5 * IQR) & dfm_filtrado$V8 < (Q3 + 1.5 * IQR))
NROW(no_outliers)

[1] 213

4.2.3 Gestionar outliers: imputación

Varible V25

# Outliers V25:

p1 <- plot(imputate_outlier(dfm_filtrado, V25, method = "mean"))
p2 <- plot(imputate_outlier(dfm_filtrado, V25, method = "median"))
p3 <- plot(imputate_outlier(dfm_filtrado, V25, method = "mode"))
p4 <- plot(imputate_outlier(dfm_filtrado, V25, method = "capping"))

grid.arrange(p1, p2, p3, p4, ncol = 2)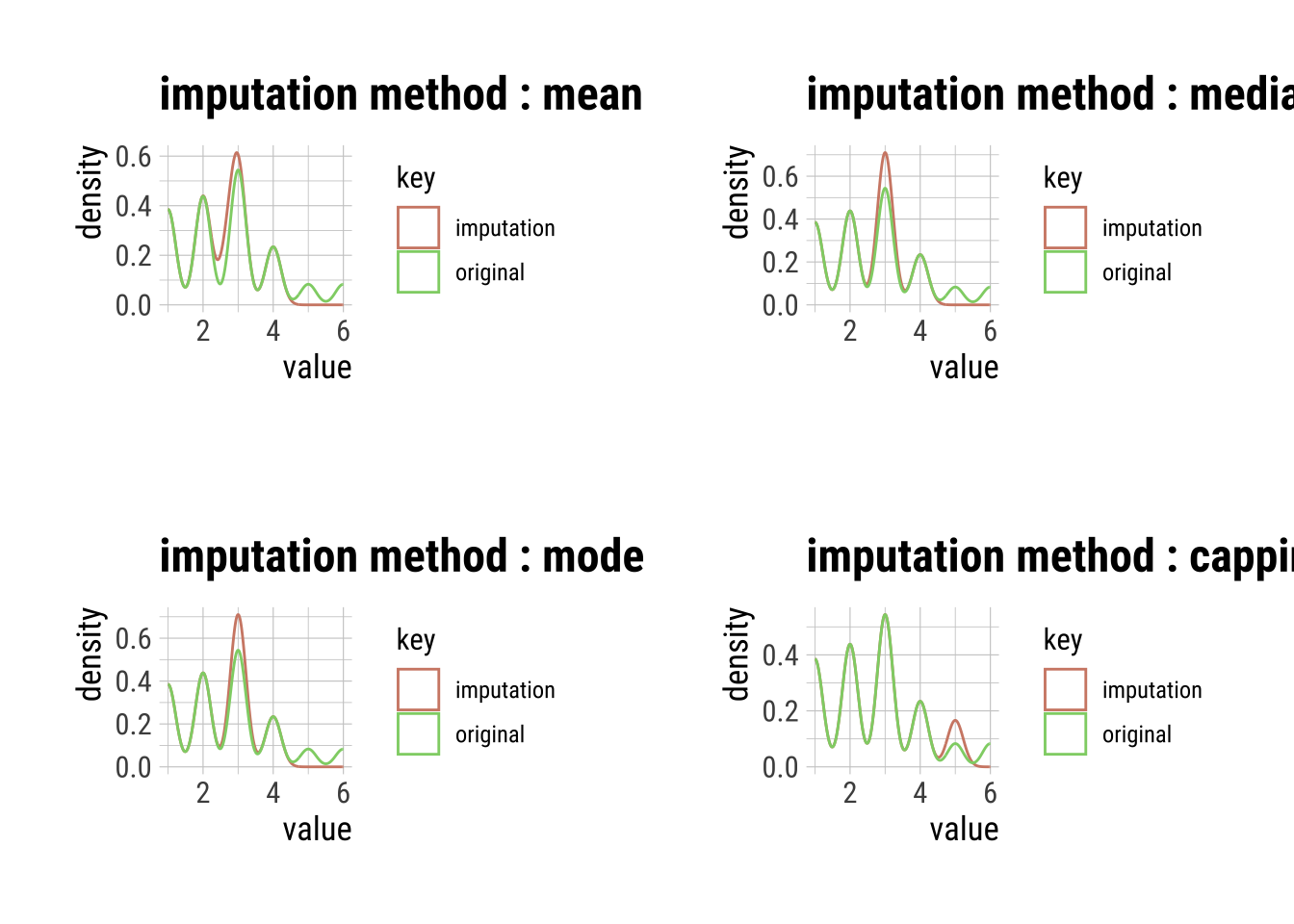

# Nos quedamos con la transformación más respetuosa
V25_imp <- imputate_outlier(dfm_filtrado, V25, method = "capping")
dfm_filtrado$V25_imp <- V25_imp

4.3 Agrupamiento (binning):

Dlookr incluye los siguientes procedimientos:

quantil (segmentación por cuartiles, usado por defecto),
equal (segmentos igual tamaño),
pretty (elige tamaños buenos-bonitos ¿?),
Otros como k-means y bclust (vía bagging y bootstrap aggregating).

4.4 Agrupamiento de la variable Edad del dataset de ejemplo

# Vemos que agrupación es más útil.
plot(binning(dfm_filtrado$Edad_imp, type = "quantile", nbins = 4))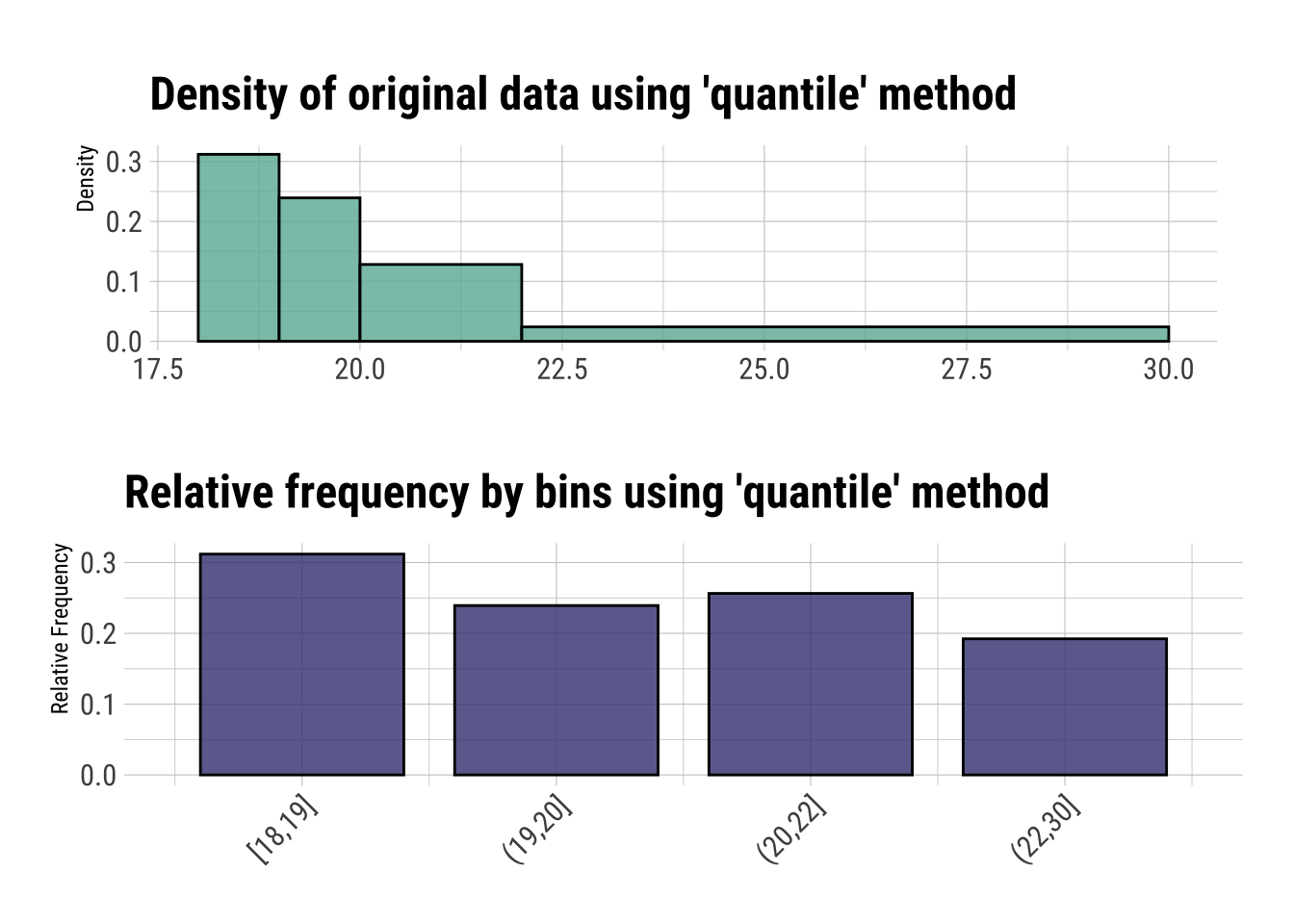

plot(binning(dfm_filtrado$Edad_imp, type = "equal", nbins = 4))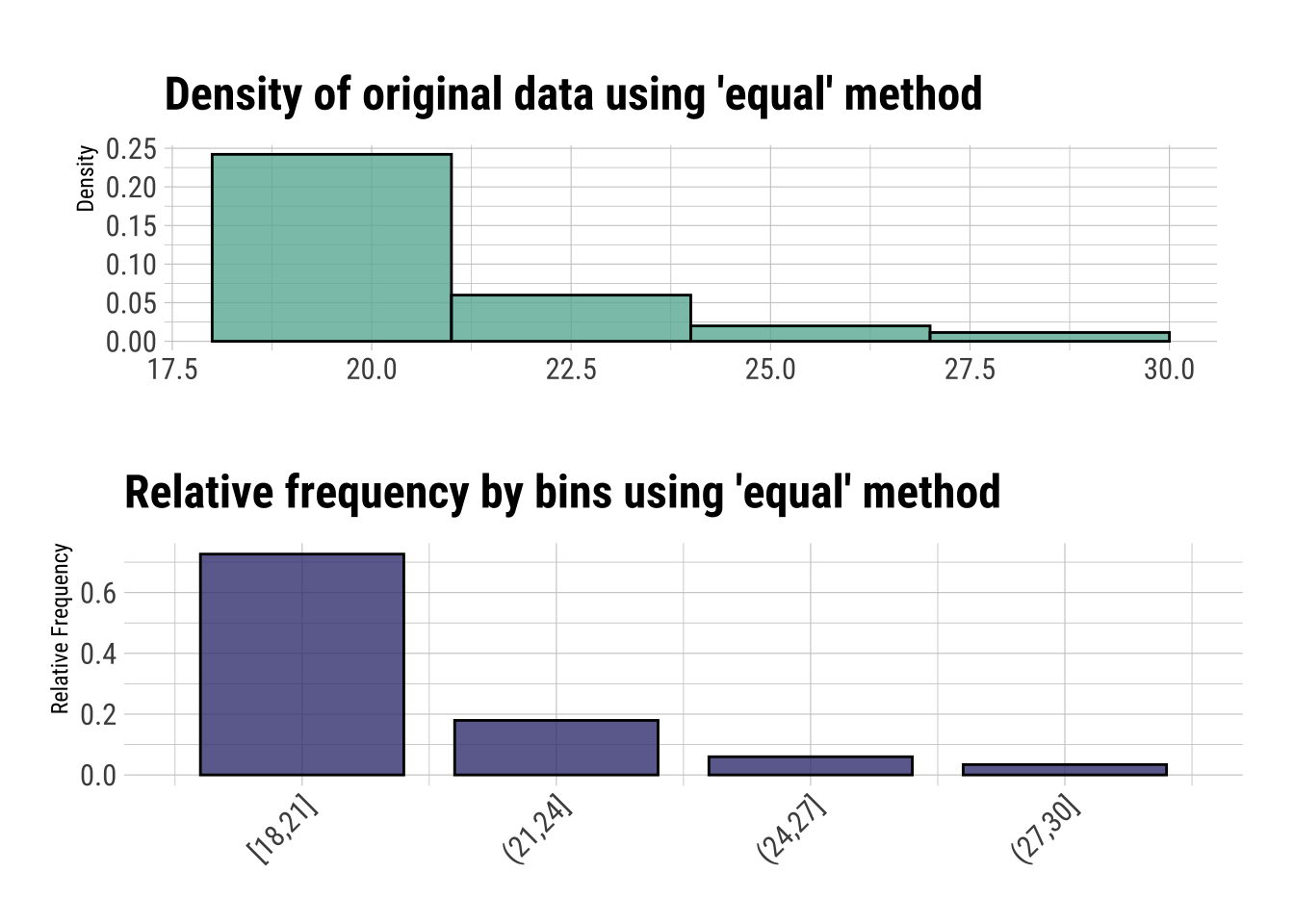

plot(binning(dfm_filtrado$Edad_imp, type = "pretty", nbins = 4))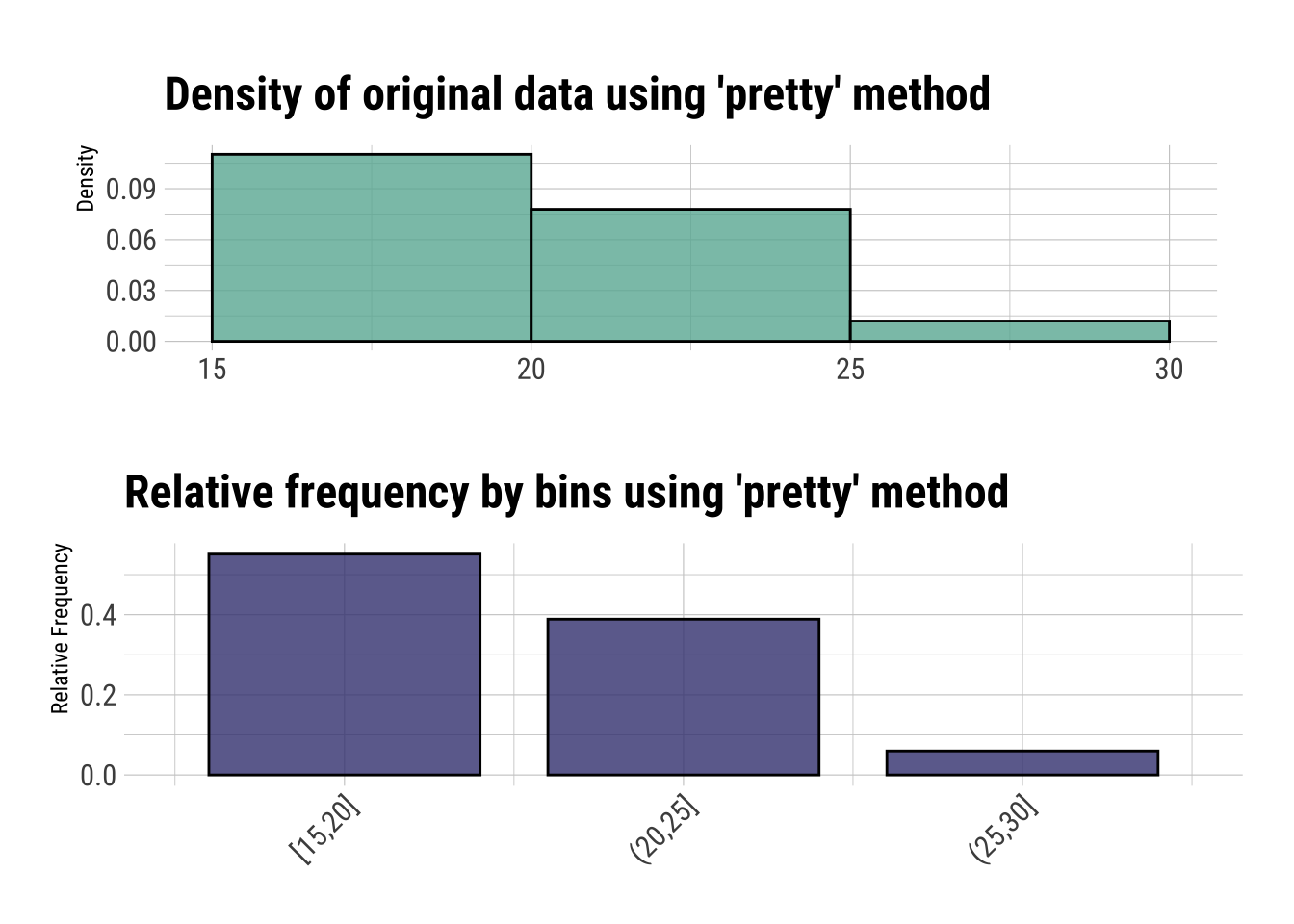

plot(binning(dfm_filtrado$Edad_imp, type = "kmeans", nbins = 4))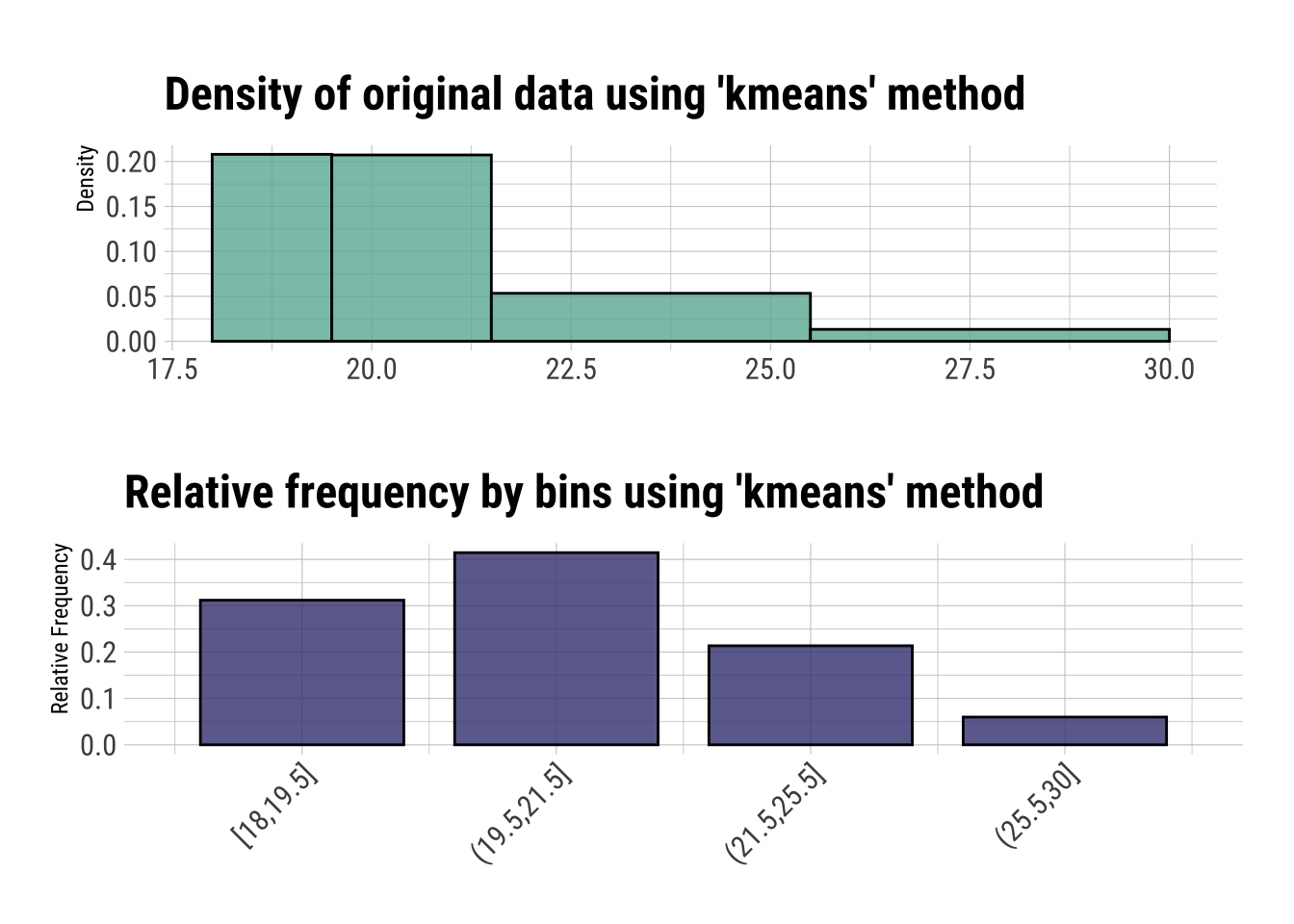

plot(binning(dfm_filtrado$Edad_imp, type = "bclust", nbins = 4))

Error in bclust(x = var, centers = n, ...) : 
  Could not find valid cluster solution in 20 replications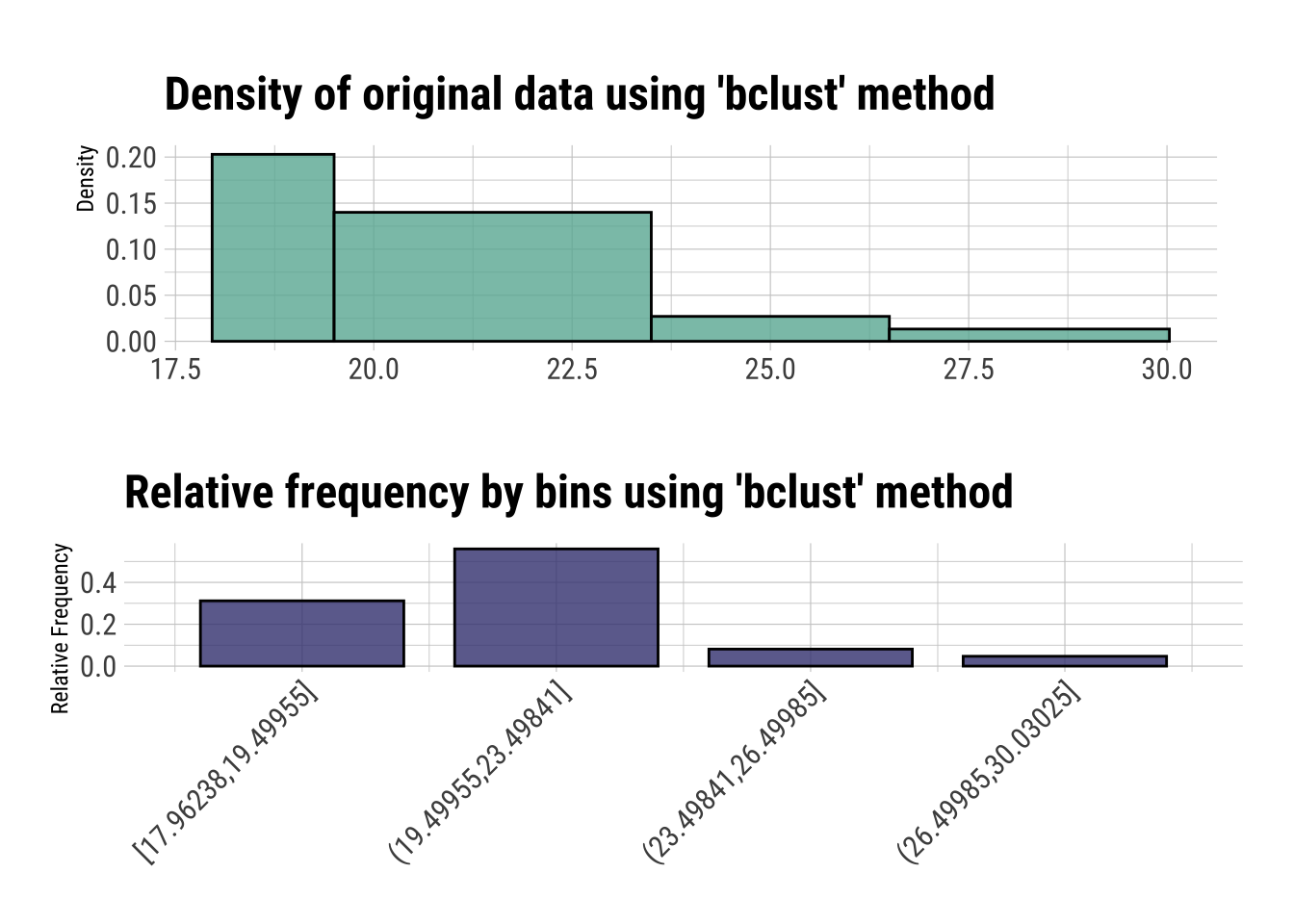

# Realizmos la agrupación

Edad_imp_cat <- (binning(dfm_filtrado$Edad_imp, nbins = 4, labels = c("18.5", "19.5", "21", ">22")))

summary(Edad_imp_cat)

  levels freq      rate
1   18.5   73 0.3119658
2   19.5   56 0.2393162
3     21   60 0.2564103
4    >22   45 0.1923077

dfm_filtrado$Edad_imp_cat <- Edad_imp_cat # Añadimos al dataset

4.4.1 Finalización de fase de reparación

Finalizamos creado un dataframe “reparado-preparado” al que llamamos df.

# Eliminar la clase "imputation" de todas las columnas que la tengan
df <- dfm_filtrado %>%
  mutate(across(everything(), ~ if ("imputation" %in% class(.)) unclass(.) else .))


df <- select(df, -Edad, -Estudios, -Curso, -V1, -V2, -V3, -V8, -V25, -Edad_imp, -Estudios_num)

5 Exploración

5.1 Análisis exploratorio

describe(df) %>%
  flextable()

described_variables	n	mean	sd	se_mean	IQR	skewness	kurtosis	p00	p01	p05	p10	p20	p25	p30	p40	p50	p60	p70	p75	p80	p90	p95	p99	p100
N	234	123.739316	70.025290	4.57769639	119.50	-0.027602884	-1.1804054361	1	3.33	12.65	26.6	52.6	64.25	75.9	101.2	124.5	147.80	172.1	183.75	195.8	219.70	231.35	240.67	243
V4	234	3.910256	1.155534	0.07553963	2.00	-0.766118686	0.4780778260	1	1.00	1.00	2.0	3.0	3.00	4.0	4.0	4.0	4.00	5.0	5.00	5.0	5.00	5.00	6.00	6
V5	234	2.658120	1.442235	0.09428184	2.00	0.658620834	-0.2652769923	1	1.00	1.00	1.0	1.0	1.00	2.0	2.0	3.0	3.00	3.0	3.00	4.0	5.00	6.00	6.00	6
V6	234	3.047009	1.274516	0.08331769	2.00	0.400619147	-0.2519240190	1	1.00	1.00	1.3	2.0	2.00	2.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	5.35	6.00	6
V7	234	3.243590	1.244930	0.08138364	2.00	0.080152906	-0.3425049319	1	1.00	1.00	2.0	2.0	2.00	3.0	3.0	3.0	4.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V9	234	3.012821	1.334523	0.08724048	2.00	0.358878340	-0.3614489787	1	1.00	1.00	1.0	2.0	2.00	2.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	6.00	6.00	6
V10	234	3.034188	1.263089	0.08257068	2.00	0.231713064	-0.3284358486	1	1.00	1.00	1.0	2.0	2.00	2.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V11	234	3.115385	1.228916	0.08033675	2.00	0.197868652	-0.3982602206	1	1.00	1.00	2.0	2.0	2.00	2.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V12	234	3.089744	1.258645	0.08228017	2.00	0.181179035	-0.4293692879	1	1.00	1.00	1.0	2.0	2.00	2.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V13	234	3.051282	1.289417	0.08429179	2.00	0.364215590	-0.2336716058	1	1.00	1.00	1.0	2.0	2.00	2.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	5.35	6.00	6
V14	234	3.435897	1.238749	0.08097958	1.00	-0.357380072	-0.3541814311	1	1.00	1.00	2.0	2.0	3.00	3.0	3.0	4.0	4.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V15	234	3.811966	1.263089	0.08257068	2.00	-0.607402956	-0.0004991714	1	1.00	1.00	2.0	3.0	3.00	3.0	4.0	4.0	4.00	5.0	5.00	5.0	5.00	6.00	6.00	6
V16	234	3.427350	1.238275	0.08094860	1.00	-0.050830510	-0.5162898627	1	1.00	1.00	2.0	2.0	3.00	3.0	3.0	3.5	4.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V17	234	4.034188	1.276608	0.08345446	2.00	-0.825926645	0.2035026124	1	1.00	1.00	2.0	3.0	3.00	4.0	4.0	4.0	5.00	5.0	5.00	5.0	5.00	6.00	6.00	6
V18	234	3.222222	1.215855	0.07948290	1.00	0.346332621	-0.1260630508	1	1.00	1.00	2.0	2.0	3.00	3.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V19	234	2.790598	1.085882	0.07098630	1.00	0.404826010	0.2694972529	1	1.00	1.00	1.0	2.0	2.00	2.0	3.0	3.0	3.00	3.0	3.00	4.0	4.00	5.00	6.00	6
V20	234	2.705128	1.128358	0.07376309	1.00	0.492432674	0.1374002090	1	1.00	1.00	1.0	2.0	2.00	2.0	2.0	3.0	3.00	3.0	3.00	4.0	4.00	5.00	6.00	6
V21	234	3.153846	1.176416	0.07690473	2.00	0.591107622	0.1644267528	1	1.00	1.65	2.0	2.0	2.00	3.0	3.0	3.0	3.00	3.1	4.00	4.0	5.00	5.35	6.00	6
V22	234	2.799145	1.103175	0.07211680	1.00	0.328104307	0.1536101413	1	1.00	1.00	1.0	2.0	2.00	2.0	3.0	3.0	3.00	3.0	3.00	4.0	4.00	5.00	6.00	6
V23	234	3.243590	1.278940	0.08360694	2.00	0.229919620	-0.3820108917	1	1.00	1.00	2.0	2.0	2.00	3.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	5.35	6.00	6
V24	234	3.166667	1.229990	0.08040697	2.00	0.236507946	-0.1908285242	1	1.00	1.00	2.0	2.0	2.00	3.0	3.0	3.0	3.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V26	234	3.299145	1.220462	0.07978409	2.00	0.281631270	-0.5097864314	1	1.00	2.00	2.0	2.0	2.00	3.0	3.0	3.0	3.80	4.0	4.00	4.0	5.00	5.00	6.00	6
V27	234	2.042735	1.200094	0.07845261	2.00	1.134450285	0.7886710997	1	1.00	1.00	1.0	1.0	1.00	1.0	1.0	2.0	2.00	3.0	3.00	3.0	4.00	4.35	5.67	6
V28	234	3.529915	1.161416	0.07592413	1.00	0.009776589	-0.2979449826	1	1.00	2.00	2.0	3.0	3.00	3.0	3.0	3.0	4.00	4.0	4.00	5.0	5.00	5.00	6.00	6
V29	234	3.824786	1.239230	0.08101103	2.00	-0.208491374	-0.3600970164	1	1.00	2.00	2.0	3.0	3.00	3.0	4.0	4.0	4.00	5.0	5.00	5.0	5.00	6.00	6.00	6
V30	234	2.418803	1.353674	0.08849247	2.00	0.859265896	-0.0453129281	1	1.00	1.00	1.0	1.0	1.00	1.0	2.0	2.0	2.00	3.0	3.00	3.0	5.00	5.00	6.00	6
V31	234	3.162393	1.286825	0.08412239	2.00	0.400263068	-0.2464726043	1	1.00	1.00	2.0	2.0	2.00	2.9	3.0	3.0	3.00	4.0	4.00	4.0	5.00	6.00	6.00	6
V32	234	2.888889	1.529553	0.09999001	2.00	0.624235933	-0.4185539868	1	1.00	1.00	1.0	1.0	2.00	2.0	2.0	3.0	3.00	3.0	4.00	4.0	6.00	6.00	6.00	6
V33	234	2.884615	1.329566	0.08691643	2.00	0.335087726	-0.5727894440	1	1.00	1.00	1.0	2.0	2.00	2.0	3.0	3.0	3.00	3.0	4.00	4.0	5.00	5.00	6.00	6
Estudios_imp	234	3.256410	1.553917	0.10158274	3.75	-0.296181554	-1.3212063019	1	1.00	1.00	1.0	1.0	1.25	3.0	3.0	3.0	4.00	5.0	5.00	5.0	5.00	5.00	5.00	5
V1_imp	234	3.529915	1.142790	0.07470650	1.00	-0.396105175	-0.0739802243	1	1.00	1.00	2.0	3.0	3.00	3.0	3.0	4.0	4.00	4.0	4.00	4.0	5.00	5.00	6.00	6
V2_imp	234	3.298291	1.068189	0.06982968	1.15	-0.182698164	-0.2351917728	1	1.00	1.26	2.0	2.0	2.85	3.0	3.0	3.2	4.00	4.0	4.00	4.0	4.88	5.00	5.67	6
V3_imp	234	3.271795	1.108209	0.07244592	1.20	-0.045163396	-0.2859936429	1	1.00	1.00	2.0	2.0	2.80	3.0	3.0	3.0	3.96	4.0	4.00	4.0	5.00	5.00	6.00	6
V25_imp	234	2.636752	1.225838	0.08013551	1.00	0.314342112	-0.7570215607	1	1.00	1.00	1.0	1.0	2.00	2.0	2.0	3.0	3.00	3.0	3.00	4.0	4.00	5.00	5.00	5

df %>%
  group_by(Estudios_imp) %>%
  describe(V2_imp) %>%
  flextable()

described_variables	Estudios_imp	n	mean	sd	se_mean	IQR	skewness	kurtosis	p00	p01	p05	p10	p20	p25	p30	p40	p50	p60	p70	p75	p80	p90	p95	p99	p100
V2_imp	1	59	3.111864	1.2013046	0.15639653	2.0	0.01856741	-0.4308981	1	1.000	1.00	1.48	2	2.0	2.80	3.00	3.0	3.16	4.0	4.0	4.0	5.00	5.0	5.42	6
V2_imp	2	3	3.333333	0.5773503	0.33333333	0.5	1.73205081		3	3.000	3.00	3.00	3	3.0	3.00	3.00	3.0	3.20	3.4	3.5	3.6	3.80	3.9	3.98	4
V2_imp	3	70	3.151429	1.0951465	0.13089504	2.0	0.10934420	-0.2525548	1	1.000	1.36	2.00	2	2.0	2.74	3.00	3.0	3.28	4.0	4.0	4.0	4.64	5.0	5.31	6
V2_imp	4	23	3.434783	1.2294155	0.25635085	1.5	-0.39175917	-0.8424457	1	1.088	1.46	2.00	2	2.5	3.00	3.16	3.8	4.00	4.0	4.0	4.6	5.00	5.0	5.00	5
V2_imp	5	79	3.526582	0.8576517	0.09649335	1.0	-0.38722656	0.7397921	1	1.780	2.00	2.00	3	3.0	3.00	3.44	4.0	4.00	4.0	4.0	4.0	4.20	5.0	5.22	6

df %>%
  normality() %>% # Comprueba normalidad con la prueba Shapiro-Wilk
  flextable()

vars	statistic	p_value	sample
N	0.9562546	0.0000015188396544191486	234
V4	0.8838249	0.0000000000020561624408	234
V5	0.8863687	0.0000000000029524807158	234
V6	0.9240341	0.0000000013562470984343	234
V7	0.9335932	0.0000000086901068838914	234
V9	0.9251814	0.0000000016814542823103	234
V10	0.9288132	0.0000000033668690742636	234
V11	0.9317405	0.0000000059884263505804	234
V12	0.9325104	0.0000000069853214680845	234
V13	0.9251769	0.0000000016800176075574	234
V14	0.9148418	0.0000000002598978874113	234
V15	0.9027486	0.0000000000349325953484	234
V16	0.9355735	0.0000000130301779862719	234
V17	0.8796562	0.0000000000011495727107	234
V18	0.9168904	0.0000000003717624647757	234
V19	0.9100079	0.0000000001141077887080	234
V20	0.9102824	0.0000000001194754629023	234
V21	0.9012280	0.0000000000274642760359	234
V22	0.9120669	0.0000000001614450483737	234
V23	0.9299915	0.0000000042375170032360	234
V24	0.9281714	0.0000000029734293345160	234
V26	0.9276923	0.0000000027111953519232	234
V27	0.8086474	0.0000000000000002971002	234
V28	0.9306750	0.0000000048476597145570	234
V29	0.9320748	0.0000000064016871603610	234
V30	0.8615008	0.0000000000001061045524	234
V31	0.9219612	0.0000000009244951178979	234
V32	0.8892367	0.0000000000044690584518	234
V33	0.9150422	0.0000000002690973234912	234
Estudios_imp	0.8218141	0.0000000000000011391060	234
V1_imp	0.9140676	0.0000000002273442330857	234
V2_imp	0.9453435	0.0000001082077535757260	234
V3_imp	0.9436924	0.0000000745473529992983	234
V25_imp	0.9001024	0.0000000000230207256856	234

df %>%
  group_by(Universidad) %>%
  normality() %>%
  flextable()

variable	Universidad	statistic	p_value	sample
N	A	0.96403561	0.0013801983535960782138730	133
N	B	0.74757203	0.0000000010147688865577820	71
N	C	0.95208548	0.1922070823775794412568985	30
V4	A	0.87683783	0.0000000040517988477208329	133
V4	B	0.90808749	0.0000733303888859193885594	71
V4	C	0.84453684	0.0004774794082551656764814	30
V5	A	0.89275354	0.0000000245453697247782444	133
V5	B	0.86102155	0.0000013229729061312137156	71
V5	C	0.90784437	0.0131348506524232785941386	30
V6	A	0.91991747	0.0000008068591282111012834	133
V6	B	0.91141374	0.0001010269995723580492260	71
V6	C	0.92714958	0.0412692913871410965720443	30
V7	A	0.93029878	0.0000036655459335979467769	133
V7	B	0.93024142	0.0006957244101149058978714	71
V7	C	0.91759760	0.0232460443012000132767536	30
V9	A	0.92847674	0.0000027865004839023955259	133
V9	B	0.90684191	0.0000651337693270724398757	71
V9	C	0.91099386	0.0157657526358473236427482	30
V10	A	0.93061135	0.0000038435723939834569714	133
V10	B	0.91754130	0.0001851215576853444970320	71
V10	C	0.93537086	0.0683031092485538171565906	30
V11	A	0.93271519	0.0000053048781005453905283	133
V11	B	0.91891519	0.0002126493718918261752009	71
V11	C	0.89379116	0.0059403351249021551713780	30
V12	A	0.93342004	0.0000059167074841396478588	133
V12	B	0.91661757	0.0001687468553632372441752	71
V12	C	0.92329131	0.0326754168170818592997762	30
V13	A	0.91374636	0.0000003455599987164156738	133
V13	B	0.92132451	0.0002718804218567774893915	71
V13	C	0.89886348	0.0078787770807759883312515	30
V14	A	0.92844202	0.0000027720806380172883290	133
V14	B	0.90595926	0.0000599145004169910575529	71
V14	C	0.80037974	0.0000666133571913921670830	30
V15	A	0.91714101	0.0000005484950127019236364	133
V15	B	0.88283836	0.0000076300221300262455518	71
V15	C	0.85800903	0.0009164795678727015448839	30
V16	A	0.93730188	0.0000109146774825635125216	133
V16	B	0.91112647	0.0000982474766428872786032	71
V16	C	0.90273370	0.0098030029193141420690294	30
V17	A	0.90151392	0.0000000710133575519791580	133
V17	B	0.86866841	0.0000023995991182504615515	71
V17	C	0.80423052	0.0000783703779972319140900	30
V18	A	0.91080211	0.0000002334285331896464338	133
V18	B	0.89170395	0.0000163606225813222936726	71
V18	C	0.89615424	0.0067718337013128364690329	30
V19	A	0.90370978	0.0000000935028123675656526	133
V19	B	0.90541585	0.0000569223098408791513387	71
V19	C	0.89248784	0.0055285666158467715314284	30
V20	A	0.91885508	0.0000006954629505603885433	133
V20	B	0.87743018	0.0000048644474041019310703	71
V20	C	0.87666993	0.0023662219192597147392199	30
V21	A	0.89786670	0.0000000453272731786488675	133
V21	B	0.90850558	0.0000763201458783843922828	71
V21	C	0.84186648	0.0004208781738922896917439	30
V22	A	0.90856488	0.0000001741303086676216716	133
V22	B	0.89059111	0.0000148404533498080437153	71
V22	C	0.90703679	0.0125376019585292739627613	30
V23	A	0.93028211	0.0000036562990903583990405	133
V23	B	0.91922942	0.0002195331476472392158786	71
V23	C	0.89776124	0.0074069625342661040215408	30
V24	A	0.92469579	0.0000015963296711694815773	133
V24	B	0.92956647	0.0006468464284930047162453	71
V24	C	0.91584932	0.0209602396966064759287196	30
V26	A	0.92618961	0.0000019856146138435563618	133
V26	B	0.91243494	0.0001115992657697208466404	71
V26	C	0.90448198	0.0108293607153130393844220	30
V27	A	0.83103015	0.0000000000462747128350288	133
V27	B	0.76603500	0.0000000027693812518796358	71
V27	C	0.77771930	0.0000264145048459567141847	30
V28	A	0.92528377	0.0000017390040887077237682	133
V28	B	0.91190246	0.0001059481981528283294674	71
V28	C	0.88340607	0.0033787362714365670388061	30
V29	A	0.92756960	0.0000024343665977837403132	133
V29	B	0.92233676	0.0003017519108420465396257	71
V29	C	0.84231931	0.0004299507924210789651387	30
V30	A	0.85421262	0.0000000003967882478891847	133
V30	B	0.86846633	0.0000023615503061902756999	71
V30	C	0.84027187	0.0003905139015234841671186	30
V31	A	0.92373879	0.0000013898012126415984136	133
V31	B	0.90420224	0.0000507948910778440075532	71
V31	C	0.93778946	0.0793164847164503500343002	30
V32	A	0.89451521	0.0000000302594792836326719	133
V32	B	0.86862525	0.0000023914183618488444260	71
V32	C	0.89304144	0.0056996580581570224083299	30
V33	A	0.91964187	0.0000007762704009931059733	133
V33	B	0.89873400	0.0000306724519060052927522	71
V33	C	0.88677153	0.0040484369794329538860822	30
Estudios_imp	A	0.71674065	0.0000000000000106517473927	133
Estudios_imp	B	0.09713472	0.0000000000000000009004821	71
Estudios_imp	C			30
V1_imp	A	0.91516607	0.0000004186753201931156286	133
V1_imp	B	0.92502515	0.0003991801504789449614626	71
V1_imp	C	0.74499075	0.0000075657957325261555068	30
V2_imp	A	0.94373228	0.0000314659854631234553023	133
V2_imp	B	0.95222485	0.0088320482971255276360978	71
V2_imp	C	0.86405058	0.0012385000466245349795558	30
V3_imp	A	0.94395921	0.0000326991678017866731990	133
V3_imp	B	0.93313883	0.0009543173170494910354314	71
V3_imp	C	0.92400514	0.0341124137131022242552802	30
V25_imp	A	0.90590276	0.0000001235323962377279273	133
V25_imp	B	0.87073274	0.0000028274426872482041304	71
V25_imp	C	0.90905881	0.0140899960735791345695089	30

df %>%
  normality(V15) %>%
  flextable()

vars	statistic	p_value	sample
V15	0.9027486	0.0000000000349326	234

df %>%
  plot_normality(V15)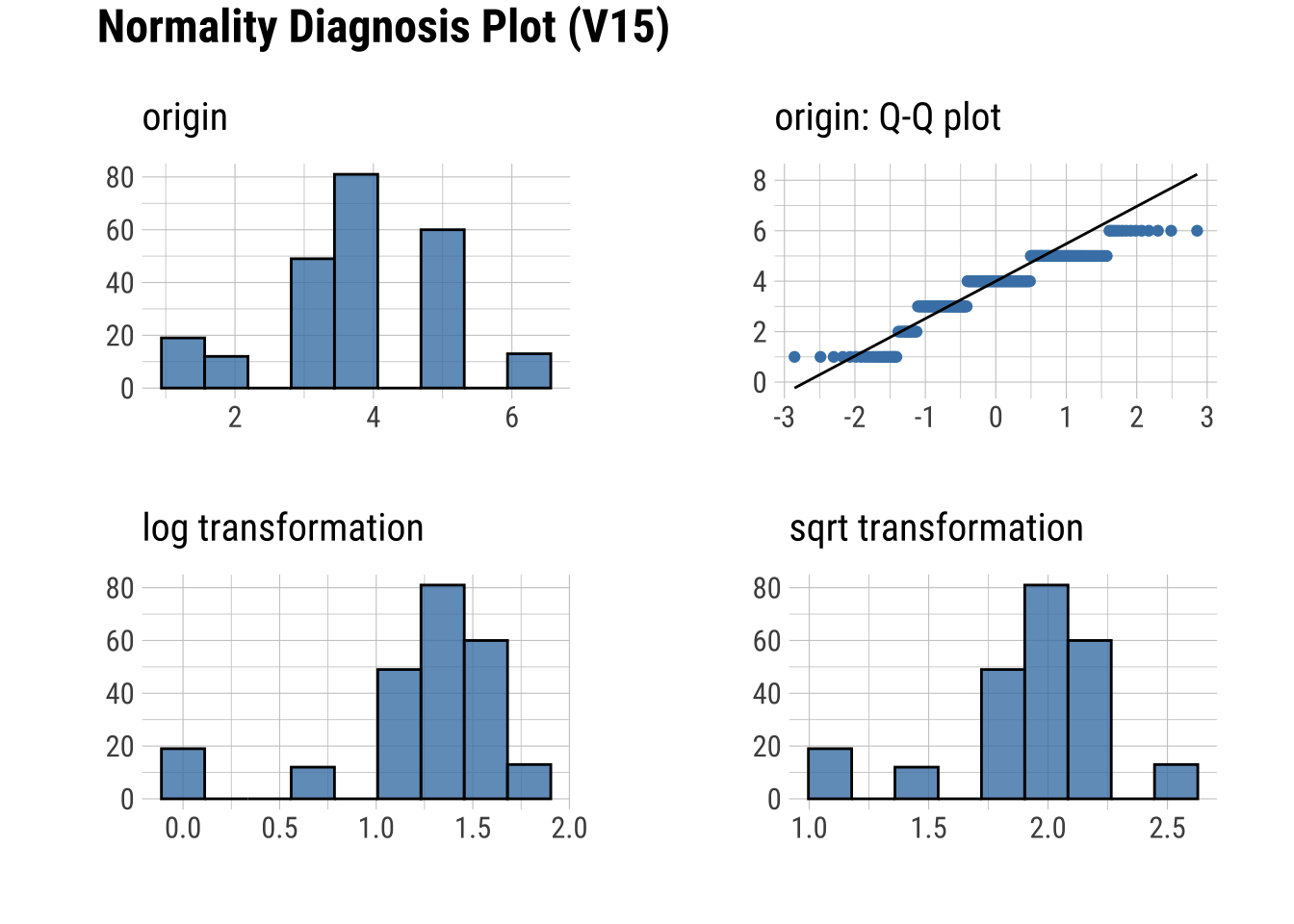

# Correlaciones

dfc <- select(df, V15, V20, V25_imp, V33) # Seleccionamos sólo algunas a modo de ejemplo

summary(correlate(dfc, method = "spearman"))

* correlation type   : generic 
* variable type      : numeric 
* correlation method : spearman 

* Matrix of Correlation
                 V15         V20     V25_imp         V33
V15      1.000000000  0.04169035 0.004279304 -0.07248045
V20      0.041690354  1.00000000 0.606086067 -0.01747726
V25_imp  0.004279304  0.60608607 1.000000000  0.03089746
V33     -0.072480451 -0.01747726 0.030897460  1.00000000

plot_correlate(dfc)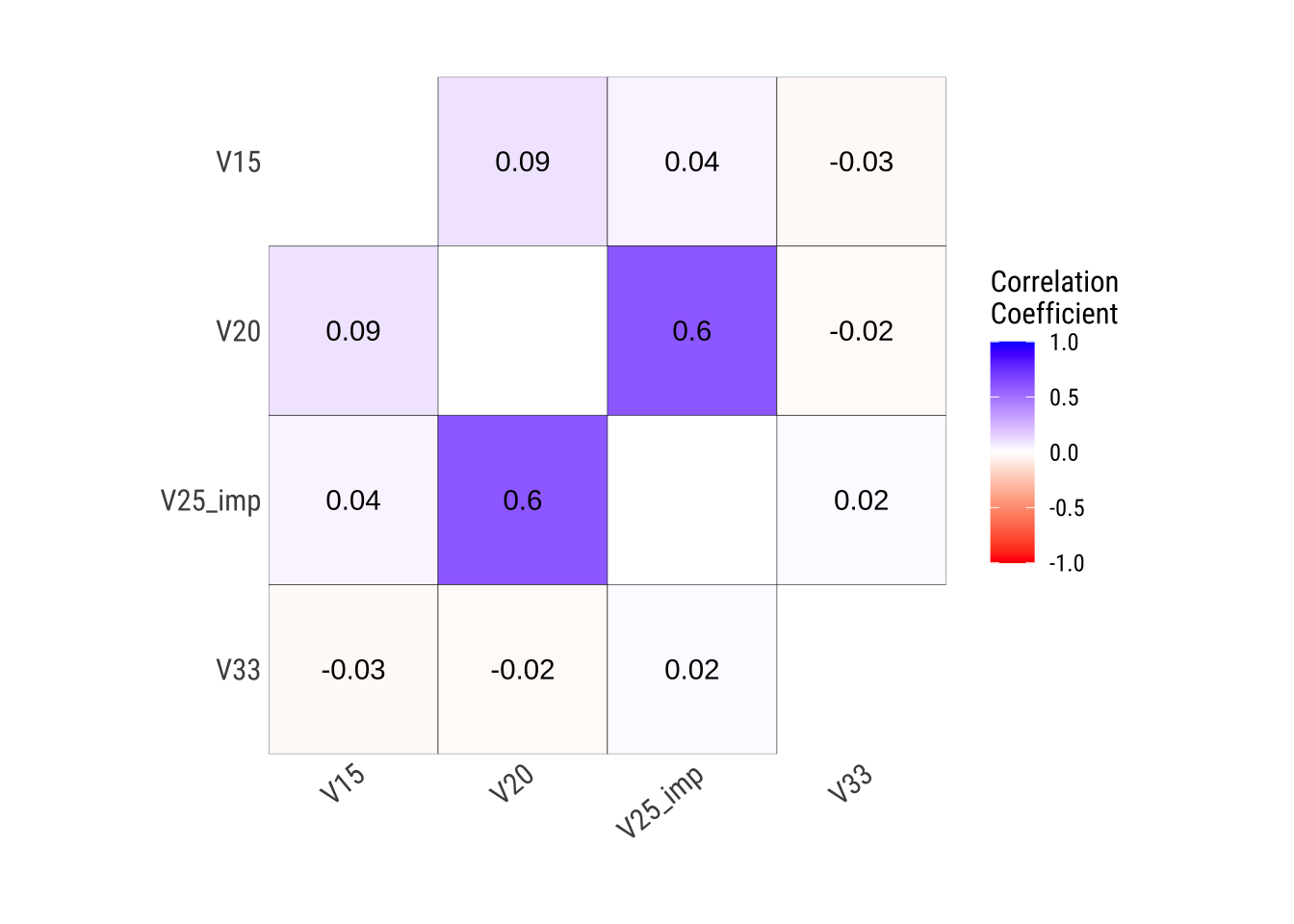

6 Informes

La función diagnose_report genera un informe que combina la mayoría de las funciones de diagnóstico.
La función eda_web_report genera un informe con análisis exploratorio de datos.

Más información sobre los informes en:

# Informe diagnóstico. Combina la mayoría de las funciones de diagnóstico
diagnose_report(df)

diagnose_web_report(df)

# Informe EDA. Genera un informe con análisis exploratorio de datos.
eda_report(df)

eda_web_report(df)